在三角形ABC中，已知
，设∠CAB＝α，
（1）求角α的值；
（2）若
，其中
，求
的值.
阅读快车系列答案科目：高中数学 来源： 题型：解答题
某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数：
①
；
②
；
③
；
④
；
⑤
.
(1) 请根据(2)式求出这个常数；
(2)根据(1)的计算结果，将该同学的发现推广为一个三角恒等式，并证明你的结论.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数
（1）求函数的最小正周期；
（2）当
时，求函数
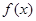的值域；
（3）先将函数
的图象向左平移
个单位得到函数
的图象，再将的图象横坐标扩大到原来的2倍纵坐标不变，得到函数
的图象，求证：直线
与的图象相切于
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
阅读下面材料：根据两角和与差的正弦公式，有
----------①
------②
由①+② 得
------③
令
有
代入③得 
．
（1）利用上述结论，试求
的值。
（2）类比上述推证方法，根据两角和与差的余弦公式，证明:
;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
;(2)
.
，从而就求得
．（2）求三角函数值问题，如果看见
，不认真思考，就直接应用公式展开
，那么就把问题化繁了，实际上这种问题应该是灵活应用公式，注意公式中“角”的任意性，“复角”的相对性，认识到
，那么要求
以及
即可，而这样做，问题就非常简捷了．
为三角形的内角，所以
. 7分
，且
，所以
，
14分
．
的值；
的值． 
中，
分别为角
的对边，且
.
的最大值.
＝
.
，求
的值。
是方程
的两根，且
求
的值.
．
的单调递增区间；
,求
的值