
【题目】动点![]() 到定点
到定点![]() 的距离比它到直线
的距离比它到直线![]() 的距离小1,设动点
的距离小1,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 的直线交曲线
的直线交曲线![]() 于
于![]() 、
、![]() 两个不同的点,过点
两个不同的点,过点![]() 、
、![]() 分别作曲线
分别作曲线![]() 的切线,且二者相交于点
的切线,且二者相交于点![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)求证: ![]() ;
;
【答案】(Ⅰ)![]() .(Ⅱ)见解析.
.(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)题设条件可转化为动点![]() 到定点
到定点![]() 的距离等于它到直线
的距离等于它到直线![]() 距离
距离
∴动点![]() 的轨迹是以
的轨迹是以![]() 为焦点,直线
为焦点,直线![]() 为准线的抛物线,可得方程为
为准线的抛物线,可得方程为![]() ;(Ⅱ)设直线
;(Ⅱ)设直线![]() 的方程为:
的方程为: ![]() ,由
,由![]() 得
得![]() ,根据韦达定理,可得
,根据韦达定理,可得![]() ,
, ![]() ,利用导数的几何意义可得两切线的方程,两方程联立可得
,利用导数的几何意义可得两切线的方程,两方程联立可得![]() ,再根据平面向量数量积公式化简可得结论.
,再根据平面向量数量积公式化简可得结论.
试题解析:(Ⅰ)由已知,动点![]() 在直线
在直线![]() 上方,条件可转化为动点
上方,条件可转化为动点![]() 到定点
到定点![]() 的距离等于它到直线
的距离等于它到直线![]() 距离
距离
∴动点![]() 的轨迹是以
的轨迹是以![]() 为焦点,直线
为焦点,直线![]() 为准线的抛物线故其方程为
为准线的抛物线故其方程为![]() .
.
(Ⅱ)证:设直线![]() 的方程为:
的方程为: ![]()
由![]() 得:
得: ![]()
设![]() ,
, ![]() ,则
,则![]() ,
, ![]()
由![]() 得:
得: ![]() ,∴
,∴![]()
∴直线![]() 的方程为:
的方程为: ![]() ①
①
直线![]() 的方程为:
的方程为: ![]() ②
②
①-②得: ![]() ,即
,即![]()
将![]() 代入①得:
代入①得: ![]()
∴![]() 故
故![]()
∴![]() ,
, ![]()
∴![]()


科目:高中数学 来源: 题型:
【题目】![]() 是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国
是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国![]() 标准采用世界卫生组织设定的最宽限值,即
标准采用世界卫生组织设定的最宽限值,即![]() 日均值在
日均值在![]() 以下空气质量为优;在
以下空气质量为优;在![]() 之间空气质量为良;在
之间空气质量为良;在![]() 之间空气质量为轻度污染.某市环保局从该市2018年上半年每天的
之间空气质量为轻度污染.某市环保局从该市2018年上半年每天的![]() 日均值数据中随机抽取20天的数据作为样本,将
日均值数据中随机抽取20天的数据作为样本,将![]() 日均值统计如下:
日均值统计如下:
日均值( |
|
|
|
|
|
天数 | 4 | 6 | 5 | 3 | 2 |
(1)在空气质量为轻度污染的数据中,随机抽取两天![]() 日均值数据,求其中恰有一天
日均值数据,求其中恰有一天![]() 日均值数据在
日均值数据在![]() 之间的概率;
之间的概率;
(2)将以上样本数据绘制成频率分布直方图(直接作图):
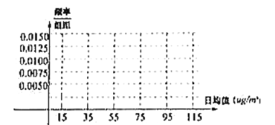
(3)该市规定:全年![]() 日均值的平均数不高于
日均值的平均数不高于![]() ,则认定该市当年的空气质量达标.现以这20天的
,则认定该市当年的空气质量达标.现以这20天的![]() 日均值的平均数来估计2018年的空气质量情况,试预测该市2018年的空气质量是否达标.
日均值的平均数来估计2018年的空气质量情况,试预测该市2018年的空气质量是否达标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司“Mobike”计划在甲、乙两座城市共投资160万元,根据行业规定,每个城市至少要投资30万元,由前期市场调研可知:甲城市收益P与投入![]() 单位:万元
单位:万元![]() 满足
满足![]() ,乙城市收益Q与投入
,乙城市收益Q与投入![]() 单位:万元
单位:万元![]() 满足
满足![]() ,设甲城市的投入为
,设甲城市的投入为![]() 单位:万元
单位:万元![]() ,两个城市的总收益为
,两个城市的总收益为![]() 单位:万元
单位:万元![]() .
.
(1)写出两个城市的总收益![]() 万元
万元![]() 关于甲城市的投入
关于甲城市的投入![]() 万元
万元![]() 的函数解析式,并求出当甲城市投资72万元时公司的总收益;
的函数解析式,并求出当甲城市投资72万元时公司的总收益;
(2)试问如何安排甲、乙两个城市的投资,才能使总收益最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市举行了一次初一学生调研考试,为了解本次考试学生的数学学科成绩情况,从中抽取部分学生的分数(满分为100分,得分取正整数,抽取学生的分数均在![]() 之内)作为样本(样本容量
之内)作为样本(样本容量![]() )进行统计,按照
)进行统计,按照![]() 的分组方法作出频率分布直方图,并作出了样本分数的茎叶图(茎叶图中仅列出了得分在
的分组方法作出频率分布直方图,并作出了样本分数的茎叶图(茎叶图中仅列出了得分在![]() 的数据].
的数据].

(Ⅰ)求频率分布直方图中的![]() 的值,并估计学生分数的中位数;
的值,并估计学生分数的中位数;
(Ⅱ)字在选取的样本中,从成绩在80分以上(含80分)的学生中随机抽取2名学生,求所抽取的2名学生中恰有一人得分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们学校是一所有着悠久传统文化的学校,我们学校全名叫重庆外国语学校(Chongqing Foreign Language School),又名四川外国语大学附属外国语学校,简称“重外”,1981年,被定为四川省首批办好的重点中学;1997年,被列为重庆市教委首批办好的直属重点中学之一;2001年被国家教育部指定为20%高三学生享有保送资格的全国十三所学校之一,今年我校保送取得了非常辉煌的成绩,目前为止,包括清华大学,北京大学在内目前共保送122名同学,其中北京大学,南开大学,北京外国语大学保送的人数成公差为正数的等差数列,三个学校保送人数之和为24人,三个学校保送学生人数之积为312,则北京外国语大学保送的人数为(以上数据均来自于学校官网)( )
A.10B.11C.13D.14
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() ,
,![]() 是以
是以![]() 为直径的圆上一段圆弧,
为直径的圆上一段圆弧,![]() 是以
是以![]() 为直径的圆上一段圆弧,
为直径的圆上一段圆弧,![]() 是以
是以![]() 为直径的圆上一段圆弧,三段弧构成曲线
为直径的圆上一段圆弧,三段弧构成曲线![]() .则下面说法正确的是( )
.则下面说法正确的是( )

A.曲线![]() 与
与![]() 轴围成的面积等于
轴围成的面积等于![]()
B.![]() 与
与![]() 的公切线方程为:
的公切线方程为:![]()
C.![]() 所在圆与
所在圆与![]() 所在圆的交点弦方程为:
所在圆的交点弦方程为:![]()
D.用直线![]() 截
截![]() 所在的圆,所得的弦长为
所在的圆,所得的弦长为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
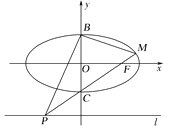
【题目】如图,已知椭圆O: ![]() 的右焦点为F,点B,C分别是椭圆O的上、下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.
的右焦点为F,点B,C分别是椭圆O的上、下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.
(1)当直线PM过椭圆的右焦点F时,求△FBM的面积;
(2)记直线BM,BP的斜率分别为k1,k2,求证:k1·k2为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com