
分析 函数$f(x)=\sqrt{2}(sinx+cosx)$=2sin(x+$\frac{π}{4}$),依次对各结论考查可得答案.
解答 解:函数$f(x)=\sqrt{2}(sinx+cosx)$=2sin(x+$\frac{π}{4}$),
对于①:$α∈(-\frac{π}{2},0)$,可得α+$\frac{π}{4}$∈($-\frac{π}{4},\frac{π}{4}$),不存在$f(α)=\sqrt{2}$;∴①不对.
对于②:函数f(x)的对称轴方程为:x+$\frac{π}{4}$=$\frac{π}{2}+kπ$,可得x=$kπ+\frac{π}{4}$,当k=-1时,可得图象关于直线$x=-\frac{3π}{4}$对称.∴②对.
对于③:函数f(x+ϕ)=2sin(x+ϕ+$\frac{π}{4}$),当ϕ+$\frac{π}{4}$=kπ,即ϕ=$kπ-\frac{π}{4}$时,图象关于坐标原点成中心对称;
∴存在φ∈R,使函数f(x+ϕ)的图象关于坐标原点成中心对称;∴③对.
对于④:函数f(x)=2sin(x+$\frac{π}{4}$)的图象向左平移$\frac{π}{4}$,可得:2sin(x$+\frac{π}{4}$+$\frac{π}{4}$)=2cos2x,不能得到y=-2cosx的图象.∴④不对.
故答案为:②③.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于中档题.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
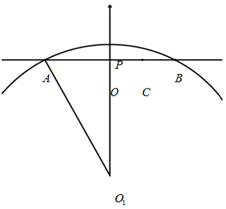 如图,某处立交桥为一段圆弧AB.已知地面上线段AB=40米,O为AB中点.桥上距离地面最高点P,且OP高5米.工程师在OB中点C处发现他的正上方桥体有裂缝.需临时找根直立柱,立于C处,用于支撑桥体.求直立柱的高度.(精确到0.01米).
如图,某处立交桥为一段圆弧AB.已知地面上线段AB=40米,O为AB中点.桥上距离地面最高点P,且OP高5米.工程师在OB中点C处发现他的正上方桥体有裂缝.需临时找根直立柱,立于C处,用于支撑桥体.求直立柱的高度.(精确到0.01米).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
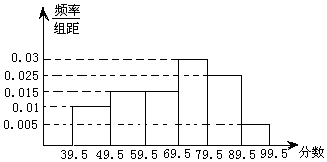 如图,从参加环保知识竞赛的学生中抽出80名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
如图,从参加环保知识竞赛的学生中抽出80名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,f(x)≠f(x+T) | B. | ?x∈R,f(x)≠f(x+T) | C. | ?x∈R,f(x)=f(x+T) | D. | ?x∈R,f(x)=f(x+T) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com