练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．已知点A，B为圆C：x2+y2=4上的任意两点，且|AB|＞2，若线段AB中点组成的区域为M，在圆C内任取一点，则该点落在区域M内的概率为$\frac{3}{4}$．

    分析 由题意，求出线段AB中点组成的区域为M为半径为$\sqrt{3}$的同心圆，利用几何概型的公式得到所求．

    解答 解：由题意，线段AB中点组成的区域M为以原点为圆心，$\sqrt{3}$为半径的圆，由几何概型的公式得到$\frac{π（\sqrt{3}）^{2}}{π×4}=\frac{3}{4}$；
    故答案为：$\frac{3}{4}$．

    点评 本题考查了几何概型的概率求法；关键是求出区域M的面积．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    13．若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1、F2，线段F1F2被抛物线y2=2bx的焦点分成5：3两段，则此双曲线的离心率为（　　）
    A．$\sqrt{2}$B．$\frac{2\sqrt{3}}{3}$C．$\frac{3\sqrt{2}}{4}$D．$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知复数z=x+yi（x，y∈R）满足z•$\overline{z}$+（1-2i）•z+（1+2i）•$\overline{z}$=3．求复数z在复平面内对应的点的轨迹．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．设函数f（x）=|x-a|+|2x+2|-5（a∈R）．
    （Ⅰ）试比较f（-1）与f（a）的大小；
    （Ⅱ）当a=-5时，求函数f（x）的图象与轴围成的图形面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．把正整数排列成如图甲的三角形数阵，然后擦去第偶数行的奇数和第奇数行中的偶数，得到如图乙的三角数阵，再把图乙中的数按从小到大的顺序排成一列，得到数列{an}，若an=623，则n的值为324．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

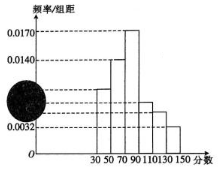    1．2017年省内事业单位面向社会公开招聘工作人员，为保证公平竞争，报名者需要参加笔试和面试两部分，且要求笔试成绩必须大于或等于90分的才有资格参加面试，90分以下（不含90分）则被淘汰．现有2000名竞聘者参加笔试，参加笔试的成绩按区间[30，50），[50，70），[70，90），[90，110），[110，130），[130，150]分段，其频率分布直方图如下图所示（频率分布直方图有污损），但是知道参加面试的人数为500，且笔试成绩在的人数为1440．
    （1）根据频率分布直方图，估算竞聘者参加笔试的平均成绩；
    （2）若在面试过程中每人最多有5次选题答题的机会，累计答题或答错3题即终止答题．答对3题者方可参加复赛．已知面试者甲答对每一个问题的概率都相同，并且相互之间没有影响．若他连续三次答题中答对一次的概率为$\frac{9}{64}$，求面试者甲答题个数X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知函数$f（x）=\left\{{\begin{array}{l}{\frac{x+1}{x-1}-1，x＞1}\\{2-{e^x}，x≤1}\end{array}}\right.$，若函数h（x）=f（x）-mx-2有且仅有一个零点，则实数m的取值范围是（-∞，-e]∪{0}∪{-$\frac{1}{2}$}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

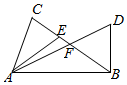    5．如图，F为线段BC的中点，CE=2EF，$DF=\frac{3}{5}AF$，设$\overrightarrow{AC}=a$，$\overrightarrow{AB}=b$，试用a，b表示$\overrightarrow{AE}$，$\overrightarrow{AD}$，$\overrightarrow{BD}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．对于函数$f（x）=\sqrt{2}（sinx+cosx）$，给出下列四个命题：
    ①存在$α∈（-\frac{π}{2}，0）$，使$f（α）=\sqrt{2}$；
    ②函数f（x）的图象关于直线$x=-\frac{3π}{4}$对称；
    ③存在φ∈R，使函数f（x+ϕ）的图象关于坐标原点成中心对称；
    ④函数f（x）的图象向左平移$\frac{π}{4}$就能得到y=-2cosx的图象．
    其中正确命题的序号是②③．

    查看答案和解析>>

    同步练习册答案