
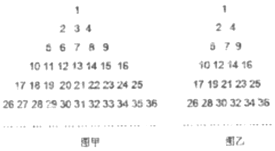
分析 根据题意,分析图乙,可得其第k行有k个数,则前k行共有$\frac{k(k+1)}{2}$个数,第k行最后的一个数为k2,从第三行开始,以下每一行的数,从左到右都是公差为2的等差数列;进而由242<623<252,可得623出现在第25行,又第25行第一个数为242+1=577,由等差数列的性质,可得该行第24个数为623,由前24行的数字数目,相加可得答案.
解答 解:分析图乙,可得①第k行有k个数,则前k行共有$\frac{k(k+1)}{2}$个数,
②第k行最后的一个数为k2,
③从第三行开始,以下每一行的数,从左到右都是公差为2的等差数列,
又由242<623<252,
则623出现在第25行,
第25行第一个数为242+1=577,
所以第$\frac{623-577}{2}$+1=24个数623,
则n=$\frac{24×(24+1)}{2}$+24=324
故答案为:324
点评 本题考查归纳推理的运用,关键在于分析乙图,发现每一行的数递增规律与各行之间数字数目的变化规律.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
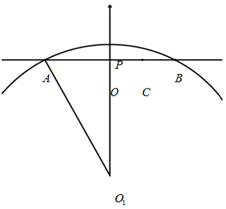 如图,某处立交桥为一段圆弧AB.已知地面上线段AB=40米,O为AB中点.桥上距离地面最高点P,且OP高5米.工程师在OB中点C处发现他的正上方桥体有裂缝.需临时找根直立柱,立于C处,用于支撑桥体.求直立柱的高度.(精确到0.01米).
如图,某处立交桥为一段圆弧AB.已知地面上线段AB=40米,O为AB中点.桥上距离地面最高点P,且OP高5米.工程师在OB中点C处发现他的正上方桥体有裂缝.需临时找根直立柱,立于C处,用于支撑桥体.求直立柱的高度.(精确到0.01米).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com