
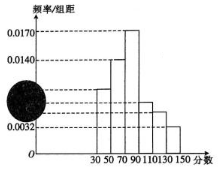
 2017��ʡ����ҵ��λ������ṫ����Ƹ������Ա��Ϊ��֤��ƽ��������������Ҫ�μӱ��Ժ����������֣���Ҫ����Գɼ�������ڻ����90�ֵIJ����ʸ�μ����ԣ�90�����£�����90�֣�����̭������2000����Ƹ�߲μӱ��ԣ��μӱ��Եijɼ�������[30��50����[50��70����[70��90����[90��110����[110��130����[130��150]�ֶΣ���Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ�����𣩣�����֪���μ����Ե�����Ϊ500���ұ��Գɼ��ڵ�����Ϊ1440��
2017��ʡ����ҵ��λ������ṫ����Ƹ������Ա��Ϊ��֤��ƽ��������������Ҫ�μӱ��Ժ����������֣���Ҫ����Գɼ�������ڻ����90�ֵIJ����ʸ�μ����ԣ�90�����£�����90�֣�����̭������2000����Ƹ�߲μӱ��ԣ��μӱ��Եijɼ�������[30��50����[50��70����[70��90����[90��110����[110��130����[130��150]�ֶΣ���Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ�����𣩣�����֪���μ����Ե�����Ϊ500���ұ��Գɼ��ڵ�����Ϊ1440������ ��1�������Ƹ�߳ɼ�������[30��50����[90��110����[110��130�����������ɴ��������Ƹ�߲μӱ��Ե�ƽ���ɼ���
��2����������ÿ�����Եĸ���Ϊp����${C}_{3}^{1}p��1-p��^{2}$=$\frac{9}{64}$�����p=$\frac{3}{4}$�������״������X�Ŀ���ȡֵΪ3��4��5���ֱ������Ӧ�ĸ��ʣ��ɴ������X���˲��к�E��X����
��� �⣺��1���辺Ƹ�߳ɼ�������[30��50����[90��110����[110��130���������ֱ�Ϊx��y��z��
��0.0170+0.0140����20��2000+x=2000-500�����x=260��
��0.0170+0.0140����20��2000+y=1440�����y=200��
0.0032��20��2000+200+z=500�����z=172��
��Ƹ�߲μӱ��Ե�ƽ���ɼ�Ϊ��
$\frac{1}{2000}$����260��40+200��100+172��120��+��0.014��60+0.017��80+0.0032��140����20=78.48���֣���
��2����������ÿ�����Եĸ���Ϊp����${C}_{3}^{1}p��1-p��^{2}$=$\frac{9}{64}$�����p=$\frac{3}{4}$��
�����״������X�Ŀ���ȡֵΪ3��4��5��
��P��X=3��=��$\frac{3}{4}$��3+��$\frac{1}{4}$��3=$\frac{7}{16}$��
P��X=4��=${C}_{3}^{2}��\frac{1}{4}����\frac{3}{4}��^{2}+{C}_{3}^{1}��\frac{3}{4}����\frac{1}{4}��^{2}��\frac{1}{4}��=\frac{45}{128}$��
P��X=5��=1-P��X=3��-P��X=4��=1-$\frac{7}{16}$-$\frac{45}{128}$=$\frac{27}{128}$��
��X���˲���Ϊ��
| X | 3 | 4 | 5 |
| P | $\frac{7}{16}$ | $\frac{45}{128}$ | $\frac{27}{128}$ |
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã�������ɢ����������ķֲ��С���ѧ����������������������������ݴ����������������ν��˼�룬���е��⣮


 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��������ABC-A1B1C1�����ⳤ��Ϊ2��D��E�ֱ���BC��BB1�е㣮
��֪��������ABC-A1B1C1�����ⳤ��Ϊ2��D��E�ֱ���BC��BB1�е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 6 | C�� | 7 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\overrightarrow{BO}=-\frac{5}{6}\overrightarrow{AB}+\frac{1}{6}\overrightarrow{AC}$ | B�� | $\overrightarrow{BO}=\frac{1}{6}\overrightarrow{AB}-\frac{1}{2}\overrightarrow{AC}$ | C�� | $\overrightarrow{BO}=\frac{5}{6}\overrightarrow{AB}-\frac{1}{6}\overrightarrow{AC}$ | D�� | $\overrightarrow{BO}=-\frac{1}{6}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com