
分析 (1)由$tan2θ=-2\sqrt{2}$,$θ∈(\frac{π}{4},\frac{π}{2})$.利用二倍角公式即可出tanθ的值;
(2)根据tanθ的值求出sinθ和cosθ,利用二倍角和和与差的公式化简可求出$\frac{{2{{cos}^2}\frac{θ}{2}-sinθ-1}}{{\sqrt{2}sin(\frac{π}{4}+θ)}}$的值.
解答 解:(1)由tan2θ=$\frac{2tanθ}{1-ta{n}^{2}θ}=-2\sqrt{2}$,$θ∈(\frac{π}{4},\frac{π}{2})$.
可得:$\sqrt{2}$tan2θ-tanθ-$\sqrt{2}$=0,
∵$θ∈(\frac{π}{4},\frac{π}{2})$.
∴tanθ=$\sqrt{2}$.
(2)由(1)可知tanθ=$\sqrt{2}$,即$\frac{sinθ}{cosθ}=\sqrt{2}$,sin2θ+cos2θ=1,
可得:sinθ=$\frac{\sqrt{6}}{3}$,cosθ=$\frac{\sqrt{3}}{3}$.
那么$\frac{{2{{cos}^2}\frac{θ}{2}-sinθ-1}}{{\sqrt{2}sin(\frac{π}{4}+θ)}}$=$\frac{cosθ-sinθ}{cosθ+sinθ}$=$\frac{\frac{\sqrt{3}}{3}-\frac{\sqrt{6}}{3}}{\frac{\sqrt{3}}{3}+\frac{\sqrt{6}}{3}}$=2$\sqrt{2}-3$.
点评 本题考查了同角三角函数的关系式的计算和二倍角公式的运用.属于基础题.


科目:高中数学 来源: 题型:解答题
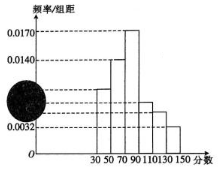 2017年省内事业单位面向社会公开招聘工作人员,为保证公平竞争,报名者需要参加笔试和面试两部分,且要求笔试成绩必须大于或等于90分的才有资格参加面试,90分以下(不含90分)则被淘汰.现有2000名竞聘者参加笔试,参加笔试的成绩按区间[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]分段,其频率分布直方图如下图所示(频率分布直方图有污损),但是知道参加面试的人数为500,且笔试成绩在的人数为1440.
2017年省内事业单位面向社会公开招聘工作人员,为保证公平竞争,报名者需要参加笔试和面试两部分,且要求笔试成绩必须大于或等于90分的才有资格参加面试,90分以下(不含90分)则被淘汰.现有2000名竞聘者参加笔试,参加笔试的成绩按区间[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]分段,其频率分布直方图如下图所示(频率分布直方图有污损),但是知道参加面试的人数为500,且笔试成绩在的人数为1440.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15千克 | B. | 16千克 | C. | 17千克 | D. | 18千克 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | MP<OM<0 | B. | OM>0>MP | C. | OM<MP<0 | D. | MP>0>OM |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ϕ | B. | {0} | C. | {0,1} | D. | $\{0,1,\sqrt{2}\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
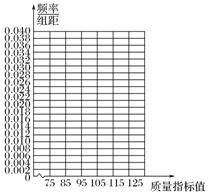 从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com