
���� ���ݺ���f��x����һ�������x=$\frac{��}{3}$���ó�f��$\frac{��}{3}$��=0���ٸ���ֱ��x=-$\frac{��}{6}$�Ǻ���f��x��ͼ���һ���Գ��ᣬ�ó�-$\frac{��}{6}$��-��=$\frac{��}{2}$+k�У�k��Z���ɴ�����ص���Сֵ���Ӧ�յ�ֵ��д��f��x�����ٸ������Һ�����ͼ�������ʽ����жϣ�
��� �⣺����f��x��=2sin����x-�գ�-1��һ�������x=$\frac{��}{3}$��
��f��$\frac{��}{3}$��=2sin��$\frac{��}{3}$��-�գ�-1=0��
��sin��$\frac{��}{3}$��-�գ�=$\frac{1}{2}$��
��$\frac{��}{3}$��-��=$\frac{��}{6}$+2k�л�$\frac{��}{3}$��-��=$\frac{5��}{6}$+2k�У�k��Z��
��ֱ��x=-$\frac{��}{6}$�Ǻ���f��x��ͼ���һ���Գ��ᣬ
��-$\frac{��}{6}$��-��=$\frac{��}{2}$+k��k��Z��
�֦أ�0��|��|���У�
��ص���Сֵ��$\frac{2}{3}$����=-$\frac{11��}{18}$��
��f��x��=2sin��$\frac{2}{3}$x+$\frac{11��}{18}$��-1��
��x��[-$\frac{4��}{3}$��-$\frac{��}{6}$]ʱ��$\frac{2}{3}$x+$\frac{11��}{18}$��[-$\frac{5��}{18}$��$\frac{��}{2}$]��
��f��x����[-$\frac{4��}{3}$��-$\frac{��}{6}$]�ϵ����������ʢ���ȷ��
��x��[-$\frac{5��}{6}$��$\frac{5��}{3}$]ʱ��$\frac{2}{3}$x+$\frac{11��}{18}$��[$\frac{��}{18}$��$\frac{31��}{18}$]��
��f��x����[-$\frac{5��}{6}$��$\frac{5��}{3}$]�ϲ��������ʢڴ���
��x=$\frac{7��}{12}$ʱ��sin��$\frac{2}{3}$x+$\frac{11��}{18}$��=sin��=0���ʢ���ȷ��
��$x=\frac{-4��}{3}$ʱ��sin��$\frac{2}{3}$x+$\frac{11��}{18}$��=sin��-$\frac{5��}{18}$���١�1���ʢܴ���y
�ʴ�Ϊ���٢ۣ�
���� ���⿼����y=Asin����x+�գ���ͼ�������ʣ����Һ��������ʣ������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ?x��R��f��x����f��x+T�� | B�� | ?x��R��f��x����f��x+T�� | C�� | ?x��R��f��x��=f��x+T�� | D�� | ?x��R��f��x��=f��x+T�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ?����R��ʹ��sin2��+cos2��=1 | B�� | ?����R��ʹ��sin2��+cos2����1 | ||
| C�� | ?����R��ʹ��sin2��+cos2��=1 | D�� | ?����R��ʹ��sin2��+cos2����1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
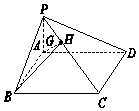 ��ͼ��HΪ����P-ABCD����PC�����ȷֵ㣬��PH=$\frac{1}{2}$HC����G��AH�ϣ�AG=mAH���ı���ABCDΪƽ���ı��Σ���G��B��P��D�ĵ㹲�棬��ʵ��m���ڣ�������
��ͼ��HΪ����P-ABCD����PC�����ȷֵ㣬��PH=$\frac{1}{2}$HC����G��AH�ϣ�AG=mAH���ı���ABCDΪƽ���ı��Σ���G��B��P��D�ĵ㹲�棬��ʵ��m���ڣ�������| A�� | $\frac{1}{4}$ | B�� | $\frac{4}{3}$P��D | C�� | $\frac{3}{4}$ | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\frac{1}{2}$ | C�� | -1 | D�� | $-\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com