
分析 (1)使用反证法证明;
(2)使用分析法证明.
解答 证明:(1)假设$\frac{1+b}{a},\frac{1+a}{b}$都不小于2,
则$\frac{1+b}{a}≥2,\frac{1+a}{b}≥2$,
∵a>0,b>0,∴1+b≥2a,1+a≥2b,
两式相加得:2+a+b≥2(a+b),解得 a+b≤2,
这与已知a+b>2矛盾,
故假设不成立,
∴$\frac{1+b}{a},\frac{1+a}{b}$中至少有一个小于2.
(2)∵$\frac{1}{b}$-$\frac{1}{a}$>1,a>0,∴0<b<1,
要证$\sqrt{1+a}$>$\frac{1}{\sqrt{1-b}}$,只需证$\sqrt{1+a}$•$\sqrt{1-b}$>1,
只需证1+a-b-ab>1,只需证a-b-ab>0,即$\frac{a-b}{ab}$>1.
即$\frac{1}{b}$-$\frac{1}{a}$>1.这是已知条件,
所以原不等式成立.
点评 本题考查了不等式的证明,属于中档题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | MP<OM<0 | B. | OM>0>MP | C. | OM<MP<0 | D. | MP>0>OM |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
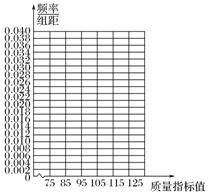 从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\sqrt{2}$) | B. | (-$\sqrt{2}$,0) | C. | (-∞,0)∪($\sqrt{2}$,+∞) | D. | (-∞,-$\sqrt{2}$)∪($\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 197 | 198 | 201 | 204 | 205 |
| y | 1 | 3 | 6 | 7 | m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com