
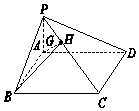
 如图,H为四棱锥P-ABCD的棱PC的三等分点,且PH=$\frac{1}{2}$HC,点G在AH上,AG=mAH.四边形ABCD为平行四边形,若G,B,P,D四点共面,则实数m等于( )
如图,H为四棱锥P-ABCD的棱PC的三等分点,且PH=$\frac{1}{2}$HC,点G在AH上,AG=mAH.四边形ABCD为平行四边形,若G,B,P,D四点共面,则实数m等于( )| A. | $\frac{1}{4}$ | B. | $\frac{4}{3}$P,D | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
分析 若G,B,P,D四点共面,则G即为AH与平面PBD的交点,连接AC,BD交于点O,连接PO,则G即为PO与AH的交点,取HC的中点E,连接OE,结合三角形的中位线定理,可得答案.
解答 解:如下图所示: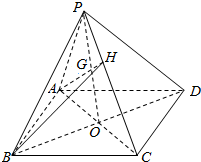
若G,B,P,D四点共面,
则G即为AH与平面PBD的交点,
连接AC,BD交于点O,连接PO,
则G即为PO与AH的交点,如下图所示: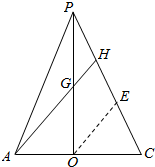
在截面PAC中,O为AC的中点,H为PC的三等分点,取HC的中点E,连接OE,
则OE=$\frac{1}{2}$AH=2GH,
故GH=$\frac{1}{4}$AH,
即AG=$\frac{3}{4}$AH,
故m=$\frac{3}{4}$.
故选:C
点评 本题考查的知识点是四点共面问题,将空间问题转化为平面问题,是解答的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | ϕ | B. | {0} | C. | {0,1} | D. | $\{0,1,\sqrt{2}\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<3} | B. | {x|x≥5} | C. | {x|3≤x≤5} | D. | {x|3<x≤5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\sqrt{2}$) | B. | (-$\sqrt{2}$,0) | C. | (-∞,0)∪($\sqrt{2}$,+∞) | D. | (-∞,-$\sqrt{2}$)∪($\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
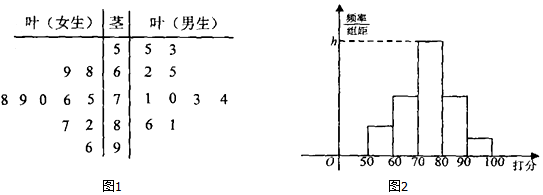
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com