
分析 (Ⅰ)通过讨论x的范围,得到关于x的不等式组,解出即可;
(Ⅱ)根据[-$\frac{5}{3}$,1]⊆(-a-3,-a+3),得到关于a的不等式组,解出即可.
解答 解:(Ⅰ)∵f(x)=|x-1|+2|x+1|≤4,
∴$\left\{\begin{array}{l}{x≥1}\\{x-1+2x+2≤4}\end{array}\right.$或$\left\{\begin{array}{l}{-1<x<1}\\{-x+1+2x+2≤4}\end{array}\right.$或$\left\{\begin{array}{l}{x≤-1}\\{-x+1-2x-2≤4}\end{array}\right.$,
解得:{x|-$\frac{5}{3}$≤x≤1};
(Ⅱ)在-$\frac{5}{3}$≤x≤1时,不等式|x+3|+|x+a|<x+6等价于|x+a|<3,
等价于-a-3<x<-a+3,
从而[-$\frac{5}{3}$,1]⊆(-a-3,-a+3),
故$\left\{\begin{array}{l}{1<-a+3}\\{-a-3<-\frac{5}{3}}\end{array}\right.$,
解得:{a|-$\frac{4}{3}$<a<2}.
点评 本题考查了解绝对值不等式问题,考查分类讨论思想以及集合的包含关系,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | 15千克 | B. | 16千克 | C. | 17千克 | D. | 18千克 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ϕ | B. | {0} | C. | {0,1} | D. | $\{0,1,\sqrt{2}\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
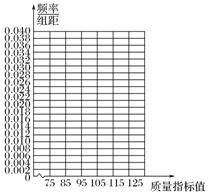 从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 6 | C. | 8 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com