练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．如果一组数据a1，a2，a3，a4，a5，a6的方差是2，那么另一组数据2a1，2a2，2a3，2a4，2a5，2a6的方差是（　　）
    A．2B．6C．8D．-2

    分析 根据平均数与方差的概念进行求解即可．

    解答 解：设数据a1，a2，a3，a4，a5，a6的平均数为$\overline{x}$，方差是s2=2，
    则数据2a1，2a2，2a3，2a4，2a5，2a6的平均数为2$\overline{x}$，
    ∴方差为s′2=$\frac{1}{6}$[（2a1-2$\overline{x}$）2+…+（2a6-2$\overline{x}$）2]
    =4×$\frac{1}{6}$[（a1-$\overline{x}$）2+…+（a6-$\overline{x}$）2]
    =4s2
    =4×2=8．
    故选：C．

    点评 本题主要考查了平均数与方差的定义和应用问题，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    17．（Ⅰ）求值：$\frac{{tan150°cos{{210}°}sin（{-60°}）}}{{sin（-30°）cos{{120}°}}}$；
    （Ⅱ）化简：$\frac{sin（-α）cos（π+α）tan（2π+α）}{cos（2π+α）sin（π-α）tan（-α）}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

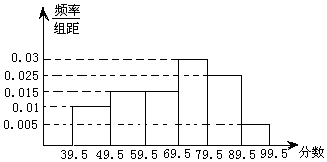    18．如图，从参加环保知识竞赛的学生中抽出80名，将其成绩（均为整数）整理后画出的频率分布直方图如下：观察图形，回答下列问题：
    （1）[79.5，89.5）这一组的频数、频率分别是多少？
    （2）估计这次环保知识竞赛的及格率（60分及以上为及格）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知集合A={-1，0，1}，B={x|0≤x≤1}，则A∩（∁RB）=（　　）
    A．-1B．{-1}C．{1}D．{-1，1}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．用数学归纳法证明1+a1+a2+…+an+1=f（n）（n∈N*），在验证n=1时，左边所得的项为（　　）
    A．1B．1+a1+a2C．2D．1+a1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．设函数f（x）=|x-1|+2|x+1|
    （Ⅰ）解不等式f（x）≤4；
    （Ⅱ）当f（x）≤4时，|x+3|+|x+a|＜x+6，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．关于直线l，m及平面α，β，下列命题正确的是（　　）
    A．若l∥α，α∩β=m，则l∥mB．若l⊥α，l∥β，则α⊥β
    C．若l∥m，m?α，则l∥αD．若l∥α，m⊥l，则m⊥α

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知定义在R上的函数f（x）周期为T（常数），则命题“?x∈R，f（x）=f（x+T）”的否定是（　　）
    A．?x∈R，f（x）≠f（x+T）B．?x∈R，f（x）≠f（x+T）C．?x∈R，f（x）=f（x+T）D．?x∈R，f（x）=f（x+T）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．某企业节能降耗技术改造后，在生产某产品过程中记录的产量x（吨）与相应的生产能耗y（吨）的几组对应数据如表所示：
    x3456
    y2.534a
    若根据表中数据得出y关于x的线性回归方程为y=0.7x+0.35，则表中a的值为4.5．

    查看答案和解析>>

    同步练习册答案