
分析 (1)根据二倍角公式即可求出A,再根据三角形的内角和定理即可求出C,
(2)根据余弦定理和b2+c2=a-bc+2,求出a,再根据两角差的正弦公式即可求出sinC,再由正弦公式和三角形的面积公式即可求出
解答 解:(1)因为cosA-cos2A=0,
所以2cos2A-cosA-1=0,
解得cosA=-$\frac{1}{2}$,cosA=1(舍去).
所以$A=\frac{2}{3}π$,
又$B=\frac{π}{4}$,
所以$C=\frac{π}{12}$.
(2)在△ABC中,因为$A=\frac{2}{3}π$,由余弦定理
所以a2=b2+c2-2bccosA=b2+c2+bc,
又b2+c2=a-bc+2,
所以a2=a+2,
所以a=2,
又因为$sinC=sin\frac{π}{12}=sin({\frac{π}{3}-\frac{π}{4}})=\frac{{\sqrt{6}-\sqrt{2}}}{4}$,
由正弦定理$\frac{c}{sinC}=\frac{a}{sinA}$
得$c=\frac{{3\sqrt{2}-\sqrt{6}}}{3}$,
所以${S_{△ABC}}=\frac{1}{2}ac•sinB=1-\frac{{\sqrt{3}}}{3}$.
点评 本题考查了正弦定理和余弦定理三角形的面积公式以及二倍角公式和两角差的正弦公式,考查了学生的运算能力和转化能力,属于中档题


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
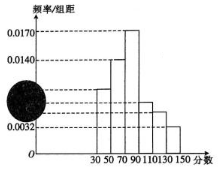 2017年省内事业单位面向社会公开招聘工作人员,为保证公平竞争,报名者需要参加笔试和面试两部分,且要求笔试成绩必须大于或等于90分的才有资格参加面试,90分以下(不含90分)则被淘汰.现有2000名竞聘者参加笔试,参加笔试的成绩按区间[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]分段,其频率分布直方图如下图所示(频率分布直方图有污损),但是知道参加面试的人数为500,且笔试成绩在的人数为1440.
2017年省内事业单位面向社会公开招聘工作人员,为保证公平竞争,报名者需要参加笔试和面试两部分,且要求笔试成绩必须大于或等于90分的才有资格参加面试,90分以下(不含90分)则被淘汰.现有2000名竞聘者参加笔试,参加笔试的成绩按区间[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]分段,其频率分布直方图如下图所示(频率分布直方图有污损),但是知道参加面试的人数为500,且笔试成绩在的人数为1440.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
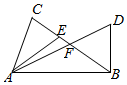 如图,F为线段BC的中点,CE=2EF,$DF=\frac{3}{5}AF$,设$\overrightarrow{AC}=a$,$\overrightarrow{AB}=b$,试用a,b表示$\overrightarrow{AE}$,$\overrightarrow{AD}$,$\overrightarrow{BD}$.
如图,F为线段BC的中点,CE=2EF,$DF=\frac{3}{5}AF$,设$\overrightarrow{AC}=a$,$\overrightarrow{AB}=b$,试用a,b表示$\overrightarrow{AE}$,$\overrightarrow{AD}$,$\overrightarrow{BD}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15千克 | B. | 16千克 | C. | 17千克 | D. | 18千克 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ϕ | B. | {0} | C. | {0,1} | D. | $\{0,1,\sqrt{2}\}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com