
 如图,点E是菱形ABCD所在平面外一点,EA⊥平面ABCD,EA∥FB∥GD,∠ABC=60°,EA=AB=2BF=2GD.
如图,点E是菱形ABCD所在平面外一点,EA⊥平面ABCD,EA∥FB∥GD,∠ABC=60°,EA=AB=2BF=2GD.分析 (I)连结BD交AC于O,取EC的中点M,连结OM,GM,建立空间坐标系,利用向量证明GM⊥AE,GM⊥AC可得GM⊥平面EAC,于是平面平面EAC⊥平面ECG;
(II)求出平面EBC和平面BCF的法向量,计算两法向量的夹角即可得出二面角的大小.
解答  (I)证明:连结BD交AC于O,取EC的中点M,连结OM,GM,
(I)证明:连结BD交AC于O,取EC的中点M,连结OM,GM,
∵O,M分别是AC,EC的中点,
∴OM∥EA,又∵EA⊥平面ABCD,
∴OM⊥平面ABCD,
以O为原点,以OB,OC,OM为坐标轴建立空间坐标系如图所示:
设BF=1,则A(0,-1,0),C(0,1,0),E(0,-1,2),D(-$\sqrt{3}$,0,0),
G(-$\sqrt{3}$,0,1),M(0,0,1),
∴$\overrightarrow{AC}$=(0,2,0),$\overrightarrow{AE}$=(0,0,2),$\overrightarrow{GM}$=($\sqrt{3}$,0,0),
∴$\overrightarrow{GM}•\overrightarrow{AC}$=0,$\overrightarrow{GM}•\overrightarrow{AE}$=0,
∴GM⊥AC,GM⊥AE,又AE∩AC=A,
∴GM⊥平面EAC,又GM?平面ECG,
∴平面EAC⊥平面ECG.
(II)解:B($\sqrt{3}$,0,0),F($\sqrt{3}$,0,1),
∴$\overrightarrow{EC}$=(0,2,-2),$\overrightarrow{EB}$=($\sqrt{3}$,1,-2),$\overrightarrow{EF}$=($\sqrt{3}$,1,-1),
设平面BEC的法向量为$\overrightarrow{m}$=(x1,y1,z1),平面FEC的法向量为$\overrightarrow{n}$=(x2,y2,z2),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{EC}=0}\\{\overrightarrow{m}•\overrightarrow{EB}=0}\end{array}\right.$,$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EC}=0}\\{\overrightarrow{n}•\overrightarrow{EF}=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{2{y}_{1}-2{z}_{1}=0}\\{\sqrt{3}{x}_{1}+{y}_{1}-2{z}_{1}=0}\end{array}\right.$,$\left\{\begin{array}{l}{2{y}_{2}-2{z}_{2}=0}\\{\sqrt{3}{x}_{2}+{y}_{2}-{z}_{2}=0}\end{array}\right.$,
令x1=$\sqrt{3}$得$\overrightarrow{m}$=($\sqrt{3}$,3,3),令y2=1得$\overrightarrow{n}$=(0,1,1).
∴cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{6}{\sqrt{21}•\sqrt{2}}$=$\frac{\sqrt{42}}{7}$.
∴二面角B-PC-F的余弦值为$\frac{\sqrt{42}}{7}$.
点评 本题考查了面面垂直的判定,空间向量在立体几何中的应用,空间角的计算,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 当a>1时,函数y=ax是增函数,因为2>1,所以函数y=2x是增函数,这种推理是合情推理 | |
| B. | 在平面中,对于三条不同的直线a,b,c,若a∥b,b∥c,则a∥c,将此结论放到空间中也是如此.这种推理是演绎推理 | |
| C. | 命题$P:?{x_0}∈R,{e^{x_0}}<{x_0}$的否定是¬P:?x∈R,ex>x | |
| D. | 若分类变量X与Y的随机变量K2的观测值k越小,则两个分类变量有关系的把握性越小 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
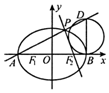 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,左、右焦点为F1,F2,点M为椭圆C上的任意一点,$\overrightarrow{M{F_1}}•\overrightarrow{M{F_2}}$的最小值为2.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,左、右焦点为F1,F2,点M为椭圆C上的任意一点,$\overrightarrow{M{F_1}}•\overrightarrow{M{F_2}}$的最小值为2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $±\frac{3}{5}$ | D. | $±\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com