
分析 4a•4b=32,利用指数幂的运算性质可得:a+b=$\frac{5}{2}$.利用基本不等式的性质可得:3ab≤3$(\frac{a+b}{2})^{2}$,即可得出.
解答 解:∵4a•4b=32,
∴22a+2b=25,
∴a+b=$\frac{5}{2}$.
又a,b∈R*,
∴3ab≤3$(\frac{a+b}{2})^{2}$=$\frac{75}{16}$,当且仅当a=b=$\frac{5}{4}$时取等号.
故答案分别为:$\frac{75}{16}$,$\frac{5}{4}$.
点评 本题考查了指数幂的运算性质、基本不等式的性质,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{19}{3}$ | B. | $\frac{31}{3}$ | C. | -$\frac{19}{3}$ | D. | -$\frac{31}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
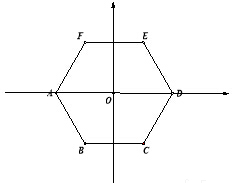 已知正六边形ABCDEF的边长是2,以正六边形中心为原点,以对角线AD所在的直线为x轴,如图建立平面直角坐标系.
已知正六边形ABCDEF的边长是2,以正六边形中心为原点,以对角线AD所在的直线为x轴,如图建立平面直角坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com