
(本小题满分13分)(Ⅰ)若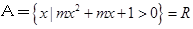 ,求实数
,求实数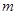 的取值范围;
的取值范围;
(Ⅱ)二次函数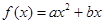 ,满足
,满足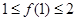 ,
,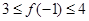 ,求
,求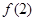 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:解答题
定义:若函数 对于其定义域内的某一数
对于其定义域内的某一数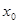 ,有
,有 ,则称
,则称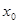 是
是 的一个不动点. 已知函数
的一个不动点. 已知函数 .
.
(1)当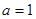 ,
,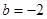 时,求函数
时,求函数 的不动点;
的不动点;
(2)若对任意的实数b,函数 恒有两个不动点,求实数
恒有两个不动点,求实数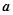 的取值范围;
的取值范围;
(3)在(2)的条件下,若 图象上两个点A、B的横坐标是函数
图象上两个点A、B的横坐标是函数 的不动点,且线段AB的中点C在函数
的不动点,且线段AB的中点C在函数 的图象上,求实数b的最小值.
的图象上,求实数b的最小值.
(参考公式:若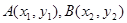 ,则线段AB的中点坐标为
,则线段AB的中点坐标为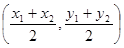 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
设平面直角坐标系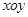 中,设二次函数
中,设二次函数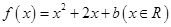 的图象与两坐标轴有三个交点,经过这三个交点的圆记为
的图象与两坐标轴有三个交点,经过这三个交点的圆记为 .求:
.求:
(Ⅰ)求实数 的取值范围;
的取值范围;
(Ⅱ)求圆 的方程;
的方程;
(Ⅲ)问圆 是否经过某定点(其坐标与b 无关)?请证明你的结论.
是否经过某定点(其坐标与b 无关)?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)某公司试销一种新产品,规定试销时销售单价不低于成本单价500元/件,又不高于800元/件,经试销调查,发现销售量y(件)与销售单价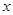 (元/件)之间,可近似看做一次函数
(元/件)之间,可近似看做一次函数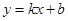 的关系(图象如图所示).
的关系(图象如图所示).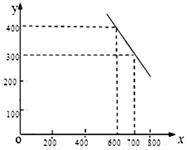
(1)根据图象,求一次函数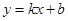 的表达式;
的表达式;
(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元:
①求S关于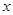 的函数表达式;
的函数表达式;
②求该公司可获得的最大毛利润,并求出此时相应的销售单价.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
依法纳税是每个公民应尽的义务,国家征收个人工资、薪金所得税是分段计算的:总收入不超过2 000元的,免征个人工资、薪金所得税;超过2 000元部分需征税,设全月纳税所得额(所得额指工资、薪金中应纳税的部分)为x,x=全月总收入-2 000元,税率如表所示:
| 级数 | 全月应纳税所得额x | 税率 |
| 1 | 不超过500元部分 | 5% |
| 2 | 超过500元至2 000元部分 | 10% |
| 3 | 超过2 000元至5 000元部分 | 15% |
| … | … | … |
| 9 | 超过100 000元部分 | 45% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com