
解:如图1-4-6,此题是考查空间直角坐标,球坐标,柱坐标的概念,要能借此区分三个坐标,找到它们的相同和不同点.
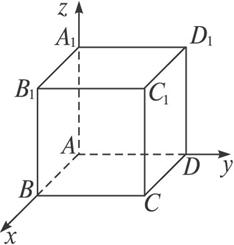
图1-4-6
C1点的(x,y,z)分别对应着CD、BC、CC1,C1点的(ρ,θ,z)分别对应着CA、∠DAC、CC1,C1点的(r,φ,θ)分别对应着AC1、∠A1AC1、∠BAC.
∴C1点的空间直角坐标为(14,6,10),C1点的柱坐标为(![]() ,arctan
,arctan![]() ,10),C1点的球坐标为(
,10),C1点的球坐标为(![]() ,arctan
,arctan![]() ).
).
深化升华 另外,点B的空间直角坐标为(14,0,0),柱坐标为(14,0,0),球坐标为(14,![]() ,0);点A1的空间直角坐标为(0,0,10),柱坐标为(0,0,10),球坐标为(10,0,0).
,0);点A1的空间直角坐标为(0,0,10),柱坐标为(0,0,10),球坐标为(10,0,0).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 已知长方体ABCD-A1B1C1D1中,AB=2,BC=4,AA1=4,点M是棱D1C1的中点.
已知长方体ABCD-A1B1C1D1中,AB=2,BC=4,AA1=4,点M是棱D1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 已知长方体ABCD-A1B1C1D1中,DA=DD1=1,DC=
已知长方体ABCD-A1B1C1D1中,DA=DD1=1,DC=| 2 |
| AE |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.
如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com