Question

8．某医学院读书协会欲研究昼夜温差大小与患感冒人数多少之间的关系，该协会分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数，得到如图频数分布直方图：
该协会确定的研究方案是：先从这六组数据中选取2组，用剩下的4组数据求线性回归方程，再用被选取的2组数据进行检验．

（1）记选取的2组数据相隔的月份数为X，若是相邻2组的数据，则X=0，求X的分布列及数学期望；
（2）已知选取的是1月与6月的两组数据．
（i）请根据2至5月份的数据，求出就诊人数y关于昼夜温差x的线性回归方程；
（ii）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人，则认为得到的线性回归方程是理想的，试问该协会所得线性回归方程是否理想？
（参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$），$\widehat{a}$=$\overline{y}$-b$\overline{x}$．

Answer 1

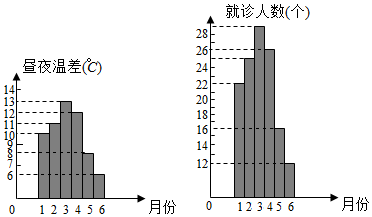
分析 （1）本题是一个古典概型，试验发生包含的事件是从6组数据中选取2组数据共有C₆²种情况，求出X的分布列及数学期望即可；
（2）（i）根据所给的数据，求出x，y的平均数，根据求线性回归方程系数的方法，求出系数b，把b和x，y的平均数，代入求a的公式，做出a的值，写出线性回归方程．
（ii）根据所求的线性回归方程，预报当自变量为10和6时的y的值，把预报的值同原来表中所给的10和6对应的值做差，差的绝对值不超过2，得到线性回归方程理想．

解答 解：（1）X可能的取值为0，1，2，3，4，
P（X=0）=$\frac{5}{15}$=$\frac{1}{3}$，P（X=1）=$\frac{4}{{C}_{6}^{2}}$=$\frac{4}{15}$，P（X=2）=$\frac{3}{{C}_{6}^{2}}$=$\frac{1}{5}$，
P（X=3）=$\frac{2}{{C}_{6}^{2}}$=$\frac{2}{15}$，P（X=4）=$\frac{1}{{C}_{6}^{2}}$=$\frac{1}{15}$，
∴X的分布列是：

X	0	1	2	3	4
P	$\frac{1}{3}$	$\frac{4}{15}$	$\frac{1}{5}$	$\frac{2}{15}$	$\frac{1}{15}$

∴EX=$\frac{4}{15}$+$\frac{2}{5}$+$\frac{6}{15}$+$\frac{4}{15}$=$\frac{4}{3}$；
（2）（i）由数据求得$\overline{x}$=11，$\overline{y}$=24，
由公式求得b=$\frac{18}{7}$，再由$\widehat{a}$=$\overline{y}$-b$\overline{x}$，
求得a=-$\frac{30}{7}$，
∴y关于x的线性回归方程为y?=$\frac{18}{7}$x-$\frac{30}{7}$；
（ii）当x=10时，y=$\frac{150}{7}$，x=6时，y=$\frac{78}{7}$，
|$\frac{150}{7}$-22|=$\frac{4}{7}$＜2，|$\frac{78}{7}$-14|=$\frac{6}{7}$＜2．
∴该小组所得线性回归方程是理想的．

点评 本题考查线性回归方程的求法，考查等可能事件的概率，考查线性分析的应用，考查解决实际问题的能力，是一个综合题目，这种题目可以作为解答题出现在高考卷中．