
分析 根据复数的有关概念,建立方程组或不等式组进行求解即可.
解答 解:(1)当m2-3m=0,即m1=0或m2=3时,z是实数;
(2)当$\left\{\begin{array}{l}{{m}^{2}-5m+6=0}\\{{m}^{2}-3m≠0}\end{array}\right.$,得$\left\{\begin{array}{l}{m=2或m=3}\\{m≠0且m≠3}\end{array}\right.$,即m=2时,z是纯虚数;
(3)当$\left\{\begin{array}{l}{{m}^{2}-5m+6=0}\\{{m}^{2}-3m=0}\end{array}\right.$,即$\left\{\begin{array}{l}{m=2或m=3}\\{m=0或m=3}\end{array}\right.$,即m=3时,z是零.
点评 本题主要考查复数的有关概念,比较基础.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
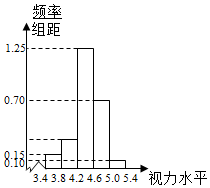 为了了解学生的视力情况,随机抽查了一批学生的视力,将抽查结果绘制成频率分布直方图(如图所示),若在[5.0,5.4]内的学生人数是10,则根据图中数据可得被样本数据的中位数是4.456;视力在[3.8,4.2]人数为12.
为了了解学生的视力情况,随机抽查了一批学生的视力,将抽查结果绘制成频率分布直方图(如图所示),若在[5.0,5.4]内的学生人数是10,则根据图中数据可得被样本数据的中位数是4.456;视力在[3.8,4.2]人数为12.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1)∪[2,+∞) | B. | (-∞,0]∪(1,+∞) | C. | (1,2] | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com