
分析 (1)在所给的等式中,令n=1,可得a0+a1+a2+…+an的值.
(2)由题意可得an为xn的系数,利用通项公式可得an=${C}_{10}^{n}$•210-2n,检验可得an的最大值.
解答 解:(1)在设${({2x+\frac{1}{2}})^{10}}={a_0}+{a_1}x+{a_2}{x^2}+…+{a_{10}}{x^{10}}$中,令x=1,可得a0+a1+a2+…+an=${(\frac{5}{2})^{10}}$.
(2)∵由题意可得an为xn的系数,∴an=${C}_{10}^{n}$•210-n•${(\frac{1}{2})}^{n}$=${C}_{10}^{n}$•210-2n,
再根据0≤n≤10,检验可得,当n=2时,an=${C}_{10}^{n}$•210-2n 取得最大值为a2=2880.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
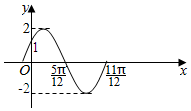 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A,右焦点为F,右准线为l,l与x轴相交于点T,且F是AT的中点.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A,右焦点为F,右准线为l,l与x轴相交于点T,且F是AT的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com