
 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A,右焦点为F,右准线为l,l与x轴相交于点T,且F是AT的中点.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A,右焦点为F,右准线为l,l与x轴相交于点T,且F是AT的中点.分析 (1)求得椭圆的准线方程,运用中点坐标公式和离心率公式,计算即可得到所求值;
(2)①过M,N作直线l的垂线,垂足分别为M1,N1,运用椭圆的第二定义(或焦半径)和三角形底面积公式计算即可得到所求比值;
②设F(c,0),则椭圆方程为$\frac{x^2}{{4{c^2}}}+\frac{y^2}{{3{c^2}}}=1$,运用点差法(或直线方程代入椭圆方程运用韦达定理),求得直线MN的斜率和方程,运用点到直线的距离公式,计算即可得到所求椭圆方程.
解答 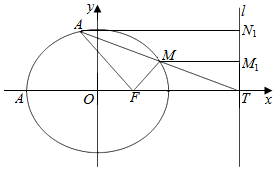 解:(1)由F是AT的中点,可得$-a+\frac{a^2}{c}=2c$,
解:(1)由F是AT的中点,可得$-a+\frac{a^2}{c}=2c$,
即(a-2c)(a+c)=0,又a、c>0,
则a=2c,可得$e=\frac{c}{a}=\frac{1}{2}$;
(2)①解法一:过M,N作直线l的垂线,
垂足分别为M1,N1,
依题意,$\frac{NF}{{N{N_1}}}=\frac{MF}{{M{M_1}}}=e$,
又NF=2MF,故NN1=2MM1,故M是NT的中点,可得$\frac{{{S_{△MNF}}}}{{{S_{△TNF}}}}=\frac{1}{2}$,
又F是AT中点,即有S△ANF=S△TNF,故$\frac{S_1}{S_2}=\frac{1}{2}$;
解法二:有a=2c,即为$b=\sqrt{3}c$,
椭圆方程为$\frac{x^2}{{4{c^2}}}+\frac{y^2}{{3{c^2}}}=1$,F(c,0),T(4c,0),
设M(x1,y1),N(x2,y2),点M在椭圆$\frac{x^2}{{4{c^2}}}+\frac{y^2}{{3{c^2}}}=1$上,即有$y_1^2=3{c^2}-\frac{3}{4}x_1^2$,$MF=\sqrt{{{({x_1}-c)}^2}+y_1^2}=\sqrt{{{({x_1}-c)}^2}+3{c^2}-\frac{3}{4}x_1^2}$
=$\sqrt{\frac{1}{4}x_1^2-2c{x_1}+4{c^2}}=|\frac{1}{2}{x_1}-2c|=2c-\frac{1}{2}{x_1}$,
同理$NF=2c-\frac{1}{2}{x_2}$,
又NF=2MF,故2x1-x2=4c,得M是N,T的中点,可得$\frac{{{S_{△MNF}}}}{{{S_{△TNF}}}}=\frac{1}{2}$,
又F是AT中点,可得S△ANF=S△TNF,则$\frac{S_1}{S_2}=\frac{1}{2}$;
②解法一:设F(c,0),则椭圆方程为$\frac{x^2}{{4{c^2}}}+\frac{y^2}{{3{c^2}}}=1$,
由①知M是N,T的中点,不妨设M(x0,y0),则N(2x0-4c,2y0),
又M,N都在椭圆上,
即有$\left\{\begin{array}{l}{\frac{{{x}_{0}}^{2}}{4{c}^{2}}+\frac{{{y}_{0}}^{2}}{3{c}^{2}}=1}\\{\frac{(2{x}_{0}-4c)^{2}}{4{c}^{2}}+\frac{4{{y}_{0}}^{2}}{3{c}^{2}}=1}\end{array}\right.$即$\left\{\begin{array}{l}{\frac{{{x}_{0}}^{2}}{4{c}^{2}}+\frac{{{y}_{0}}^{2}}{3{c}^{2}}=1}\\{\frac{({x}_{0}-2c)^{2}}{4{c}^{2}}+\frac{{{y}_{0}}^{2}}{3{c}^{2}}=\frac{1}{4}}\end{array}\right.$,
两式相减得:$\frac{x_0^2}{{4{c^2}}}-\frac{{{{({x_0}-2c)}^2}}}{{4{c^2}}}=\frac{3}{4}$,解得${x_0}=\frac{7}{4}c$,
可得${y_0}=\frac{{3\sqrt{5}}}{8}c$,故直线MN的斜率为$k=\frac{{\frac{{3\sqrt{5}}}{8}c}}{{\frac{7}{4}c-4c}}=-\frac{{\sqrt{5}}}{6}$,
直线MN的方程为$y=-\frac{{\sqrt{5}}}{6}(x-4c)$,即$\sqrt{5}x+6y-4\sqrt{5}c=0$,
原点O到直线TMN的距离为$d=\frac{{4\sqrt{5}c}}{{\sqrt{5+36}}}=\frac{{4\sqrt{5}}}{{\sqrt{41}}}c$,
依题意$\frac{{4\sqrt{5}}}{{\sqrt{41}}}c=\frac{{20\sqrt{41}}}{41}$,解得$c=\sqrt{5}$,
故椭圆方程为$\frac{x^2}{20}+\frac{y^2}{15}=1$.
解法二:设F(c,0),则椭圆方程为$\frac{x^2}{{4{c^2}}}+\frac{y^2}{{3{c^2}}}=1$,
由①知M是N,T的中点,故2x1-x2=4c,
直线MN的斜率显然存在,不妨设为k,故其方程为y=k(x-4c),与椭圆联立,
并消去y得:$\frac{x^2}{{4{c^2}}}+\frac{{{k^2}{{(x-4c)}^2}}}{{3{c^2}}}=1$,
整理得:(4k2+3)x2-32ck2x+64k2c2-12c2=0,(*)
设M(x1,y1),N(x2,y2),
即有$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=\frac{32c{k}^{2}}{3+4{k}^{2}}}\\{{x}_{1}{x}_{2}=\frac{64{k}^{2}{c}^{2}-12{c}^{2}}{3+4{k}^{2}}}\end{array}\right.$,
由$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=\frac{32c{k}^{2}}{3+4{k}^{2}}}\\{2{x}_{1}-{x}_{2}=4c}\end{array}\right.$解得$\left\{\begin{array}{l}{{x}_{1}=\frac{16c{k}^{2}+4c}{3+4{k}^{2}}}\\{{x}_{2}=\frac{16c{k}^{2}-4c}{3+4{k}^{2}}}\end{array}\right.$,
即有$\frac{{16c{k^2}+4c}}{{4{k^2}+3}}×\frac{{16c{k^2}-4c}}{{4{k^2}+3}}=\frac{{64{k^2}{c^2}-12{c^2}}}{{4{k^2}+3}}$,解之得${k^2}=\frac{5}{36}$,即$k=-\frac{{\sqrt{5}}}{6}$.
直线MN的方程为$y=-\frac{{\sqrt{5}}}{6}(x-4c)$,即$\sqrt{5}x+6y-4\sqrt{5}c=0$,
原点O到直线TMN的距离为$d=\frac{{4\sqrt{5}c}}{{\sqrt{5+36}}}=\frac{{4\sqrt{5}c}}{{\sqrt{41}}}$,
依题意$\frac{{4\sqrt{5}c}}{{\sqrt{41}}}=\frac{{20\sqrt{41}}}{41}$,解得$c=\sqrt{5}$,
故椭圆方程为$\frac{x^2}{20}+\frac{y^2}{15}=1$.
点评 本题考查椭圆的离心率的求法,注意运用椭圆的准线方程和中点坐标公式,以及离心率公式,考查椭圆的第二定义和焦半径公式,直线方程和椭圆方程联立,运用韦达定理,考查化简整理的运算能力,属于难题.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:解答题
| 家庭月收入 (单位:元) | 2千以下 | 2千~5千 | 5千~8千 | 8千~一万 | 1万~2万 | 2万以上 |
| 调查的总人数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 有二孩计划的家庭数 | 1 | 2 | 9 | 7 | 3 | 4 |
| 收入不高于8千的家庭数 | 收入高于8千的家庭数 | 合计 | |
| 有二孩计划的家庭数 | |||
| 无二孩计划的家庭数 | |||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
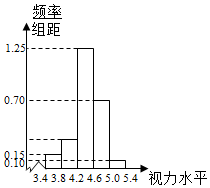 为了了解学生的视力情况,随机抽查了一批学生的视力,将抽查结果绘制成频率分布直方图(如图所示),若在[5.0,5.4]内的学生人数是10,则根据图中数据可得被样本数据的中位数是4.456;视力在[3.8,4.2]人数为12.
为了了解学生的视力情况,随机抽查了一批学生的视力,将抽查结果绘制成频率分布直方图(如图所示),若在[5.0,5.4]内的学生人数是10,则根据图中数据可得被样本数据的中位数是4.456;视力在[3.8,4.2]人数为12.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com