
| A. | $\frac{{\sqrt{6}-\sqrt{2}}}{4}$ | B. | $\frac{{\sqrt{6}}}{4}$ | C. | $\frac{{\sqrt{6}+\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
分析 已知等式利用正弦定理化简,得到关系式,利用余弦定理表示出cosC,把得出关系式整理后代入,利用基本不等式求出cosC的最小值即可.
解答 解:已知等式利用正弦定理化简得:a+$\sqrt{2}$b=2c,
两边平方得:(a+$\sqrt{2}$b)2=4c2,即a2+2$\sqrt{2}$ab+2b2=4c2,
∴4a2+4b2-4c2=3a2+2b2-2$\sqrt{2}$ab,即a2+b2-c2=$\frac{3{a}^{2}+2{b}^{2}-2\sqrt{2}ab}{4}$,
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{1}{8}$($\frac{3a}{b}$+$\frac{2b}{a}$-2$\sqrt{2}$)≥$\frac{\sqrt{6}-\sqrt{2}}{4}$(当且仅当$\frac{3a}{b}$=$\frac{2b}{a}$,即$\sqrt{3}$a=$\sqrt{2}$b时取等号),
则cosC的最小值为$\frac{\sqrt{6}-\sqrt{2}}{4}$.
故选:A.
点评 此题考查了正弦、余弦定理,以及基本不等式的运用,熟练掌握定理是解本题的关键.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | -1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
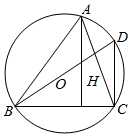 如图,已知点O是△ABC的外心,H为垂心,BD为外接圆直径.求证:
如图,已知点O是△ABC的外心,H为垂心,BD为外接圆直径.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 数学成绩xi | 90 | 100 | 115 | 130 | |
| 物理成绩yi | 60 | 65 | 70 | 75 | 80 |
| A. | 120 | B. | 122.64 | C. | 125 | D. | 127 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)在定义域上单调递减 | B. | f(x)在定义域上单调递增 | ||
| C. | f(x)是奇函数 | D. | f(x)是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{4}{5}$,13] | B. | [$\frac{{2\sqrt{5}}}{5}$,$\sqrt{13}$] | C. | [0,4] | D. | [1,$\sqrt{13}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com