练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在正三棱柱ABC-A1B1C1 中，AB=2，AA1=1，D是BC的中点，点P在平面BCC1B1内，PB1=PC1=
    		2
    ．求二面角C1-AD-C的大小．
    考点：二面角的平面角及求法
    专题：空间角
    分析：由已知条件推导出∠C1DC是二面角C1-AD-C的平面角，由此能求出二面角C1-AD-C的大小．
    解答： 解：∵正三棱柱ABC-A1B1C1 中，
    AB=2，AA1=1，D是BC的中点，
    ∴AD⊥CD，CC1⊥CD，CC1⊥AC，
    ∴AC1=
    		22+12
    =
    		5
    ，
    AD=
    		22-12
    =
    		3
    ，C1D=
    		1+1
    =
    		2
    ，
    ∴AD⊥C1D，
    ∴∠C1DC是二面角C1-AD-C的平面角，
    ∵tan∠C1DC=
    C1C
    DC
    =1    ，∴∠C1DC=45°，
    ∴二面角C1-AD-C的大小为45°．
    点评：本题考查二面角的大小的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    若sinα是5x2-7x-6=0的根，求
    sin(-α-
    3
    2
    π)•sin(
    3
    2
    π-α)•tan2(2π-α)
    cos(
    π
    2
    -α)•cos(
    π
    2
    +α)•sin(3π+α)
    的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，在四棱锥P-ABCD中，PA⊥平面ABCD，∠ABC=∠ADC=90°，∠BAD=120°，AD=AB=1，AC交BD于O点．
    （Ⅰ）求证：平面PBD⊥平面PAC；
    （Ⅱ）当点A在平面PBD内的射影G恰好是△PBD的重心时，求二面角B-PD-C的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，矩形OABC在变换T的作用下变成了平行四边形OA′B′C′，变换T所对应的矩阵为M，矩阵N是把坐标平面上的点的横坐标伸长到原来的2倍，纵坐标伸长到原来的3倍所对应的变换矩阵． 
    （Ⅰ）求（MN）-1；
    （Ⅱ）判断矩阵MN是否存在特征值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

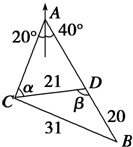    C位于A城的南偏西20°的位置，B位于A城的南偏东40°的位置，有一人距C为31千米的B处正沿公路向A城走去，走了20千米后到达D处，此时CD间的距离为21千米，问这人还要走多少千米才能到达A城？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知正方体ABCD-A′B′C′D′中，E是AA′棱的中点．求平面BEC′与平面ABCD所成的角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知等差数列{an}中，a2=5，a6=13．
    （1）求等差数列的通项公式an；
    （2）设bn=
    2
    n(an+1)
    ，求数列{bn}的前n项和Sn；
    （3）令cn=（n+1）Sn•3n，求数列{cn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求曲线y=3x4-4x3+1的拐点及凹凸区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知矩阵M=
    20
    11
    ：
    ①求矩阵M的逆矩阵M-1；
    ②求矩阵M的特征值及相应的特征向量．

    查看答案和解析>>

    同步练习册答案