
���� ��1����������ߧ�1��ֱ�����꣬��������ߧ�1�ļ����귽�̣�
��2����tan��=k��ֱ�ߧ�2����ͨ����Ϊy=k��x-1��-1����a=x-1����ֱ�ߧ�1�����ߧ�2�ĵ��ʾΪ����k2+1��a2+2ka-4=0���ɴ������ҳ���ʽ�����ֱ��ֱ�ߧ�1����б�ǣ�
��� �⣺��1�������ߧ�1�IJ�������Ϊ$\left\{\begin{array}{l}{x=1+\sqrt{5}cos��}\\{y=-2+\sqrt{5}sin��}\end{array}\right.$����Ϊ��������
�����ߧ�1��ֱ�����귽��Ϊ����x-1��2+��y+2��2=5��
��x2+y2-2x+4y=0��
�����ߧ�1�ļ����귽��Ϊ��2-2��cos��+4��sin��=0������=2cos��-4sin�ȣ�
��2����ֱ�ߧ�2�IJ�������Ϊ$\left\{\begin{array}{l}{x=1+tcos��}\\{y=-1+tsin��}\end{array}\right.$��tΪ��������
��$\frac{dx}{dt}=cos��$��$\frac{dy}{dt}=sin��$��$\frac{dy}{dx}=tan��$��
��t=0ʱ��y=-1��x=1����tan��=k��
��ֱ�ߧ�2����ͨ����Ϊy=k��x-1��-1����a=x-1��
ֱ�ߧ�2�����ߧ�1�ĵ��ʾΪ����k2+1��a2+2ka-4=0��
${a}_{1}+{a}_{2}=-\frac{2k}{{k}^{2}+1}$��${a}_{1}{a}_{2}=-\frac{4}{{k}^{2}+1}$��
��|AB|=$\sqrt{��1+{k}^{2}��[��-\frac{2k}{{k}^{2}+1}}��^{2}-4����-\frac{4}{{k}^{2}+1}��$=4��
��������$\frac{5{k}^{2}+1}{{k}^{2}+1}=4$�����k=$��\sqrt{3}$��
��ֱ��ֱ�ߧ�2����б��Ϊ60���120�㣮
���� ���⿼�����ߵļ����귽�̵�������ֱ�ߵ���б�ǵ������е��⣬����ʱҪ�������⣬ע���ҳ���ʽ�ĺ������ã�


 ��Կ���Ծ�ϵ�д�
��Կ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��һ���������������ͼ������ͼ�Ͳ���ͼ��Ϊ���Σ�����ͼ�����߲���Ϊ��Բ���ߴ���ͼ����û�����������Ϊ��������
��ͼ��һ���������������ͼ������ͼ�Ͳ���ͼ��Ϊ���Σ�����ͼ�����߲���Ϊ��Բ���ߴ���ͼ����û�����������Ϊ��������| A�� | 2+3��+4$\sqrt{2}$ | B�� | 2+�� | C�� | 4+�� | D�� | 4+2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
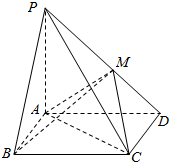 ��ͼ��������P-ABCD�У�����ABCD�Ǿ��Σ�PA��ƽ��ABCD��PA=AD=2��AB=1��BM��PD�ڵ�M����ֱ��BM��ƽ��ACM���ɵĽǵ�����ֵ��
��ͼ��������P-ABCD�У�����ABCD�Ǿ��Σ�PA��ƽ��ABCD��PA=AD=2��AB=1��BM��PD�ڵ�M����ֱ��BM��ƽ��ACM���ɵĽǵ�����ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������ABC��һ�������ױ����߷ֱ���ԲO�ཻ�ڵ�A��D��E��F��ԲO������FG��CE�ཻ�ڵ�G��
��ͼ��������ABC��һ�������ױ����߷ֱ���ԲO�ཻ�ڵ�A��D��E��F��ԲO������FG��CE�ཻ�ڵ�G���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com