
【题目】将“马”“上”“成”“功”这四个字填在一个5×5的方格表中,每个小方格内至多填1个字,“马”“上”始终按从左往右的顺序填写,“成”“功”也始终按从左往右的顺序填写,且“马”“上”必须在同一行或按从上往下的顺序在同一列,或者“成”“功”必须在同一行或按从上往下的顺序在同一列。则不同的填法种数为_______(用数字作答)。
科目:高中数学 来源: 题型:
【题目】某水果经销商为了对一批刚上市水果进行合理定价,将该水果按事先拟定的价格进行试销,得到一组销售数据,如表所示:
试销单价 | 16 | 17 | 18 | 19 | 20 |
日销售量 | 168 | 146 | 120 | 90 | 56 |
(1)已知变量![]() 具有线性相关关系,求该水果日销售量
具有线性相关关系,求该水果日销售量![]() (公斤)关于试销单价
(公斤)关于试销单价![]() (元/公斤)的线性回归方程,并据此分析销售单价
(元/公斤)的线性回归方程,并据此分析销售单价![]() 时,日销售量的变化情况;
时,日销售量的变化情况;
(2)若该水果进价为每公斤![]() 元,预计在今后的销售中,日销售量和售价仍然服从(1)中的线性相关关系,该水果经销商如果想获得最大的日销售利润,此水果的售价
元,预计在今后的销售中,日销售量和售价仍然服从(1)中的线性相关关系,该水果经销商如果想获得最大的日销售利润,此水果的售价![]()
![]() 应定为多少元?
应定为多少元?
(参考数据及公式:![]() ,
,![]() ,
,![]() ,线性回归方程
,线性回归方程![]() ,
,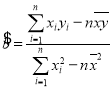 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数,则对于函数
为自然对数的底数,则对于函数![]() 有下列四个命题:
有下列四个命题:
命题1:存在实数![]() 使得函数
使得函数![]() 没有零点
没有零点
命题2:存在实数![]() 使得函数
使得函数![]() 有
有![]() 个零点
个零点
命题3:存在实数![]() 使得函数
使得函数![]() 有
有![]() 个零点
个零点
命题4:存在实数![]() 使得函数
使得函数![]() 有
有![]() 个零点
个零点
其中,正确的命题的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱.
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】桂林漓江主要景点有象鼻山、伏波山、叠彩山、芦笛岩、七星岩、九马画山,小张一家人随机从这6个景点中选取2个进行游玩,则小张一家人不去七星岩和叠彩山的概率为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.

(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,求二面角B–EC–C1的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两类水果的质量(单位:![]() )分别服从正态分布
)分别服从正态分布![]() 、
、![]() ,其正态分布的密度曲线如图所示,则下列说法正确的是( )
,其正态分布的密度曲线如图所示,则下列说法正确的是( )
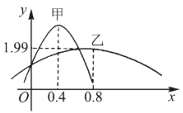
A.乙类水果的平均质量![]()
B.甲类水果的质量比乙类水果的质量更集中于平均值左右
C.甲类水果的平均质量比乙类水果的平均质量小![]()
D.乙类水果的质量服从的正态分布的参数![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 为三维空间中
为三维空间中![]() 个点组成的有限集,其中任意四点不在一个平面上,将集合
个点组成的有限集,其中任意四点不在一个平面上,将集合![]() 中的点染成白色或黑色,使得任意一个与集合
中的点染成白色或黑色,使得任意一个与集合![]() 至少交于四个点的球面具有这样的性质:这些交点中恰有一半的点为白色的.证明:集合
至少交于四个点的球面具有这样的性质:这些交点中恰有一半的点为白色的.证明:集合![]() 中所有的点均在一个球面上,
中所有的点均在一个球面上,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂利用随机数表对生产的600个零件进行抽样测试,先将600个零件进行编号,编号分别为001,002,![]() ,599,600从中抽取60个样本,如下提供随机数表的第4行到第6行:
,599,600从中抽取60个样本,如下提供随机数表的第4行到第6行:
32 21 18 34 29 78 64 54 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42
84 42 12 53 31 34 57 86 07 36 25 30 07 32 86 23 45 78 89 07 23 68 96 08 04
32 56 78 08 43 67 89 53 55 77 34 89 94 83 75 22 53 55 78 32 45 77 89 23 45
若从表中第6行第6列开始向右依次读取3个数据,则得到的第6个样本编号![]()
![]()
A. 522B. 324C. 535D. 578
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com