
分析 (Ⅰ)先求出函数f(x)的导数f′(x),由题意可知:当x≥1时,f′(x)≥0恒成立,解出a的取值范围即可.
(Ⅱ)求导函数,确定函数的单调性,比较端点的函数值,即可求得结论;
(Ⅲ)利用(Ⅱ)的结论,只要令a=1,x=$\frac{n}{n-1}$即可.
解答 解:(Ⅰ)∵$f(x)=\frac{1-x}{ax}+lnx$,∴${f^'}(x)=\frac{ax-1}{{a{x^2}}}(a>0)$,
∵函数f(x)在[1,+∞)上为增函数,
∴f′(x)≥0对任意x∈[1,+∞)恒成立.
∴ax-1≥0对任意x∈[1,+∞)恒成立,
即$a≥\frac{1}{x}$对任意x∈[1,+∞)恒成立.
∵x∈[1,+∞)时,${(\frac{1}{x})_{max}}=1$,
∴所求正实数a的取值范围是a≥1.
(Ⅱ)当a=1时,${f^'}(x)=\frac{x-1}{x^2}$,
∴当$x∈[\frac{1}{2},1)$时,f′(x)<0,
故f(x)在$[\frac{1}{2},1)$上单调递减;
∴当x∈(1,2]时,f′(x)>0,
故f(x)在(1,2]上单调递增;
∴f(x)在[$\frac{1}{2}$,2]上有唯一极小值点,且为最小值点,最小值为f(1)=0,
∵f($\frac{1}{2}$)=1-ln2,f(2)=-$\frac{1}{2}$+ln2,
∴f(x)在[$\frac{1}{2}$,2]上的最大值为1-ln2;
(Ⅲ)证明:由(Ⅰ)知lnx≥-$\frac{1-x}{x}$,
令x=$\frac{n}{n-1}$,则ln $\frac{n}{n-1}$≥$\frac{1}{n}$,
∴ln$\frac{2}{1}$+ln$\frac{3}{2}$+…+ln $\frac{n}{n-1}$>$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$,
即$lnn>\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}$.
点评 本题考查了利用导数求函数的单调区间、最值及证明不等式,充分理解导数的意义及掌握恰当分类讨论思想和转化思想是解题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{9\sqrt{3}}{2}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | 3$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{e}$+1] | B. | (-∞,$\frac{1}{e}$+1) | C. | ($\frac{1}{e}$+1,+∞) | D. | ($\frac{1}{e}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
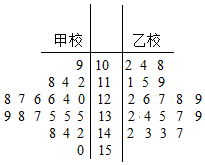
 一次数学考试后,某老师从自己所带的两个班级中各抽取6人,记录他们的考试成绩,得到如图所示的茎叶图.已知甲班6名同学成绩的平均数为82,乙班6名同学成绩的中位数为77,则x-y=( )
一次数学考试后,某老师从自己所带的两个班级中各抽取6人,记录他们的考试成绩,得到如图所示的茎叶图.已知甲班6名同学成绩的平均数为82,乙班6名同学成绩的中位数为77,则x-y=( )| A. | 3 | B. | -3 | C. | 4 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某市在对高三学生的4月理科数学调研测试的数据统计显示,全市10000名学生的成绩服从正态分布X~N(110,144),现从甲校100分以上的200份试卷中用系统抽样的方法抽取了20份试卷来分析,统计如下:
某市在对高三学生的4月理科数学调研测试的数据统计显示,全市10000名学生的成绩服从正态分布X~N(110,144),现从甲校100分以上的200份试卷中用系统抽样的方法抽取了20份试卷来分析,统计如下:| 试卷编号 | n1 | n2 | n3 | n4 | n5 | n6 | n7 | n8 | n9 | n10 |
| 试卷得分 | 109 | 118 | 112 | 114 | 126 | 128 | 127 | 124 | 126 | 120 |
| 试卷编号 | n11 | n12 | n13 | n14 | n15 | n16 | n17 | n18 | n19 | n20 |
| 试卷得分 | 135 | 138 | 135 | 137 | 135 | 139 | 142 | 144 | 148 | 150 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com