
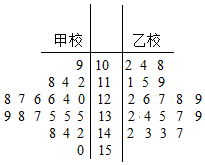
 某市在对高三学生的4月理科数学调研测试的数据统计显示,全市10000名学生的成绩服从正态分布X~N(110,144),现从甲校100分以上的200份试卷中用系统抽样的方法抽取了20份试卷来分析,统计如下:
某市在对高三学生的4月理科数学调研测试的数据统计显示,全市10000名学生的成绩服从正态分布X~N(110,144),现从甲校100分以上的200份试卷中用系统抽样的方法抽取了20份试卷来分析,统计如下:| 试卷编号 | n1 | n2 | n3 | n4 | n5 | n6 | n7 | n8 | n9 | n10 |
| 试卷得分 | 109 | 118 | 112 | 114 | 126 | 128 | 127 | 124 | 126 | 120 |
| 试卷编号 | n11 | n12 | n13 | n14 | n15 | n16 | n17 | n18 | n19 | n20 |
| 试卷得分 | 135 | 138 | 135 | 137 | 135 | 139 | 142 | 144 | 148 | 150 |
分析 (1)根据分层抽样的抽取编号为等差数列可知n5和n9的值;
(2)根据茎叶图的数据集中程度判断均值和方差;
(3)根据正态分布概率可得146分以上才能进入前15名,利用超几何分布概率公式得出分布列,从而可求出数学期望.
解答 解:(1)126分的试卷编号分别为48,88.
(2)通过茎叶图可知:甲校学生成绩的平均分高于乙校学生成绩的平均分,甲校学生成绩比较集中,乙校学生成绩比较分散.
(3)∵$\frac{15}{10000}=0.0015$,根据正态分布可知:P(74<X<146)=99.7%,
∴$P(X≥146)=\frac{1-99.7%}{2}=0.0015$,即前15名的成绩全部在146分以上(含146分).
根据茎叶图可知这40人中成绩在146分以上(含146分)的有3人,而成绩在140分以上(含140分)的有8人.
∴ξ的取值为0,1,2,3.
$P(ξ=0)=\frac{C_5^3}{C_8^3}=\frac{5}{28}$,$P(ξ=1)=\frac{C_5^2•C_3^1}{C_8^3}=\frac{15}{28}$,$P(ξ=2)=\frac{C_5^1•C_3^2}{C_8^3}=\frac{15}{56}$,$P(ξ=3)=\frac{C_3^3}{C_8^3}=\frac{1}{56}$,
所以ξ的分布列为
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{5}{28}$ | $\frac{15}{28}$ | $\frac{15}{56}$ | $\frac{1}{56}$ |
点评 本题考查了分层抽样原理,茎叶图,随机变量的分布列,属于中档题.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的最小正周期为2π | |
| B. | f(x)在[$\frac{5π}{8}$,$\frac{9π}{8}$]单调递减 | |
| C. | f(x)的图象关于直线x=-$\frac{π}{6}$对称 | |
| D. | 将f(x)的图象向右平移$\frac{π}{8}$,再向下平移$\frac{1}{2}$个单位长度后会得到一个奇函数的图象 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P,Q,R分别是棱AB,AD,AA1的中点.以△PQR为底面作一个直三棱柱,使其另一个底面的三个顶点也都在此正方体的表面上.则这个直三棱柱的体积是$\frac{3}{16}$.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P,Q,R分别是棱AB,AD,AA1的中点.以△PQR为底面作一个直三棱柱,使其另一个底面的三个顶点也都在此正方体的表面上.则这个直三棱柱的体积是$\frac{3}{16}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,一直角墙角的两边足够长,若P处有一棵树(不考虑树的粗细)与两墙的距离分别是2m和αm(0<α≤10),现用12m长的篱笆,借助墙角围成一个矩形花圃ABCD,设此矩形花圃的最大面积为u,若将这棵树围在矩形花圃内(包括边界),则函数u=f(a)(单位:m2)的图象大致是( )
如图,一直角墙角的两边足够长,若P处有一棵树(不考虑树的粗细)与两墙的距离分别是2m和αm(0<α≤10),现用12m长的篱笆,借助墙角围成一个矩形花圃ABCD,设此矩形花圃的最大面积为u,若将这棵树围在矩形花圃内(包括边界),则函数u=f(a)(单位:m2)的图象大致是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${(x+\sqrt{2})^2}+{(y+1)^2}=2$ | B. | ${(x+1)^2}+{(y+\sqrt{2})^2}=2$ | C. | ${(x-\sqrt{2})^2}+{(y-1)^2}=2$ | D. | ${(x-1)^2}+{(y-\sqrt{2})^2}=2$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,边长为2的正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AE的中点.
如图所示,边长为2的正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com