练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．已知正数a，b满足$\frac{1}{a}$+$\frac{4}{b}$=$\sqrt{ab}$，则ab的最小值为4．

    分析 正数a，b满足 $\frac{1}{a}$+$\frac{4}{b}$=$\sqrt{ab}$，$\sqrt{ab}$≥2$\sqrt{\frac{1}{a}•\frac{4}{b}}$，化为ab≥4即可得出．

    解答 解：∵正数a，b满足$\frac{1}{a}$+$\frac{4}{b}$=$\sqrt{ab}$，
    ∴$\sqrt{ab}$≥2$\sqrt{\frac{1}{a}•\frac{4}{b}}$，
    当且仅当$\frac{1}{a}$=$\frac{4}{b}$时即a=1，b=4时“=”成立，
    ∴$\sqrt{ab}$≥$\frac{4}{\sqrt{ab}}$，即ab≥4，
    故答案为：4．

    点评 本题考查了基本不等式的性质、一元二次不等式的解法，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

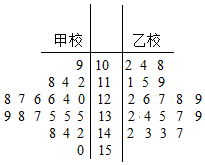    10．某市在对高三学生的4月理科数学调研测试的数据统计显示，全市10000名学生的成绩服从正态分布X～N（110，144），现从甲校100分以上的200份试卷中用系统抽样的方法抽取了20份试卷来分析，统计如下：
    试卷编号 n1 n2 n3 n4 n5 n6 n7 n8 n9 n10
    试卷得分109118112114126128127124126120
    试卷编号 n11 n12 n13 n14 n15 n16 n17 n18 n19 n20
    试卷得分135138135137135139142144148150
    （注：表中试卷编号n1＜n2＜28＜n4＜n5＜…＜n20）

    （1）列出表中试卷得分为126分的试卷编号（写出具体数据）；
    （2）该市又从乙校中也用系统抽样的方法抽取了20份试卷，将甲乙两校这40份试卷的得分制作了茎叶图（如图），试通过茎叶图比较两校学生成绩的平均分及分散程度（均不要求计算出具体值，给出结论即可）；
    （3）在第（2）问的前提下，从甲乙两校这40名学生中，从成绩在140分以上（含140分）的学生中任意抽取3人，该3人在全市前15名的人数记为ξ，求ξ的分布列和期望．
    （附：若随机变量X服从正态分布N（μ，σ2），则P（μ-σ＜X＜μ+σ）=68.3%，P（μ-2σ＜X＜μ+2σ）=95.4%，P（μ-3σ＜X＜μ+3σ）=99.7%）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．某学校高三年级有两个文科班，三个理科班，现每个班指定1人，对各班的卫生进行检  查．若每班只安排一人检查，且文科班学生不检查文科班，理科班学生不检查自己所在的班，则不同安排方法的种数是24．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知点（1，-2）和（$\frac{\sqrt{3}}{3}$，0）在直线l：ax-y-1=0（a≠0）的两侧，则直线l的倾斜角的取值范围是（　　）
    A．（$\frac{π}{4}$，$\frac{π}{3}$）B．（$\frac{π}{3}$，$\frac{2π}{3}$）C．（$\frac{2π}{3}$，$\frac{5π}{6}$）D．（0，$\frac{π}{3}$）∪（$\frac{3π}{4}$，π）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知点（1，$\frac{1}{6}$）是函数f（x）=$\frac{1}{2}$ax（a＞0，a≠1）图象上一点，等比数列{an}的前n项和为c-f（n）．数列{bn}（bn＞0）的首项为2c，前n项和满足$\sqrt{{S}_{n}}$=$\sqrt{{S}_{n-1}}$+1（n≥2）．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）若数列{$\frac{1}{{{b}_{n}b}_{n+1}}$}的前n项和为Tn，问使Tn＞$\frac{1000}{2017}$的最小正整数n是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．在平面直角坐标系xOy中，已知点P在曲线Γ：y=$\sqrt{1-\frac{{x}^{2}}{4}}$（x≥0）上，曲线Γ与x轴相交于点B，与y轴相交于点C，点D（2，1）和点E（1，0）满足$\overrightarrow{OD}$=λ$\overrightarrow{CE}$+μ$\overrightarrow{OP}$（λ，μ∈R），则λ+μ的最小值为$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．已知函数f（x）=sin（2x+φ）对一切实数满足f（$\frac{π}{6}$-x）=f（$\frac{π}{6}$+x），且-π＜φ＜0，则φ的值是-$\frac{5π}{6}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．设实数x，y满足（x+3）2+（y-4）2=4，则$\sqrt{{x}^{2}+{y}^{2}}$的最大值是7．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．角A是直角△ABC的一个内角，且$sinA=\frac{7}{8}$，则cosA=$\frac{\sqrt{15}}{8}$．

    查看答案和解析>>

    同步练习册答案