
 如图所示,边长为2的正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AE的中点.
如图所示,边长为2的正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AE的中点.分析 (1)如图,取AB中点M,连接MF,MC,由三角形中位线定理可得MF平行且等于$\frac{1}{2}BE$,结合CD平行且等于$\frac{1}{2}BE$,可得四边形MFDC为平行四边形,得MC∥FD,再由△ABC为正三角形,点M为AB中点,可得DF⊥AB,再由面面垂直的性质可得CD⊥AB,最后由线面垂直的判定得AB⊥平面CDF;
(2)在梯形BCDE中,求出三角形EDC的面积,再求出棱锥A-BCDE的高,然后利用等积法求得三棱锥F-ADC的体积.
解答 (1)证明:如图,取AB中点M,连接MF,MC,
∵M为AB中点,∴MF平行且等于$\frac{1}{2}BE$,
又CD平行且等于$\frac{1}{2}BE$,∴MF平行且等于CD,
∴四边形MFDC为平行四边形,得MC∥FD;
∵△ABC为正三角形,点M为AB中点,∴CM⊥AB,
从而DF⊥AB;
又∵平面ABC⊥平面BCDE,CD⊥BC,平面ABC∩平面BCDE=BC,
∴CD⊥平面ABC,
∴CD⊥AB,
又∵CD∩DF=D,
∴AB⊥平面CDF;
(2)解:在梯形BCDE中,
∵BE∥CD,BE=2CD=4,BE⊥BC,BC=2,
∴${S}_{△EDC}=\frac{1}{2}×2×2=2$,
过A作AO⊥BC,垂足为O,
由平面ABC⊥平面BCDE,且平面ABC∩平面BCDE=BC,
可得AO⊥平面BCDE,而AO=$\sqrt{{2}^{2}-{1}^{2}}=\sqrt{3}$.
∴${V_{F-ADC}}={V_{A-FDC}}={V_{E-FDC}}={V_{F-EDC}}=\frac{1}{2}{V_{A-EDC}}$
=$\frac{1}{2}×\frac{1}{3}×2×\sqrt{3}$=$\frac{{\sqrt{3}}}{3}$.
点评 本题考查线面垂直的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{e}$+1] | B. | (-∞,$\frac{1}{e}$+1) | C. | ($\frac{1}{e}$+1,+∞) | D. | ($\frac{1}{e}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
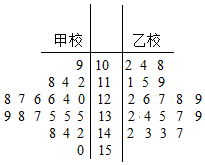 某市在对高三学生的4月理科数学调研测试的数据统计显示,全市10000名学生的成绩服从正态分布X~N(110,144),现从甲校100分以上的200份试卷中用系统抽样的方法抽取了20份试卷来分析,统计如下:
某市在对高三学生的4月理科数学调研测试的数据统计显示,全市10000名学生的成绩服从正态分布X~N(110,144),现从甲校100分以上的200份试卷中用系统抽样的方法抽取了20份试卷来分析,统计如下:| 试卷编号 | n1 | n2 | n3 | n4 | n5 | n6 | n7 | n8 | n9 | n10 |
| 试卷得分 | 109 | 118 | 112 | 114 | 126 | 128 | 127 | 124 | 126 | 120 |
| 试卷编号 | n11 | n12 | n13 | n14 | n15 | n16 | n17 | n18 | n19 | n20 |
| 试卷得分 | 135 | 138 | 135 | 137 | 135 | 139 | 142 | 144 | 148 | 150 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,一直角墙角,两边的长度足够长,若P处有一棵树与两墙的距离分别是2m和αm(0<α<10),不考虑树的粗细,现用12m长的篱笆,借助墙角围成一个矩形花圃ABCD,设此矩形花圃的最大面积为u,若将这棵树围在矩形花圃内,则函数u=f(a)(单位:m2)的图象大致是( )
如图,一直角墙角,两边的长度足够长,若P处有一棵树与两墙的距离分别是2m和αm(0<α<10),不考虑树的粗细,现用12m长的篱笆,借助墙角围成一个矩形花圃ABCD,设此矩形花圃的最大面积为u,若将这棵树围在矩形花圃内,则函数u=f(a)(单位:m2)的图象大致是( )| A. |  | B. |  | ||
| C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若事件A与事件B互斥,则事件A与事件B对立 | |
| B. | 函数y=$\sqrt{{x}^{2}+9}+\frac{1}{\sqrt{{x}^{2}+9}}$(x∈R)的最小值为2 | |
| C. | 若直线(m+1)x+my-2=0与直线mx-2y+5=0互相垂直,则m=1 | |
| D. | “p∧q为真命题”是“p∨q为真命题”的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com