
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 利用虚数单位i得性质及复数代数形式的乘除运算化简求得z,进一步求出$\overline{z}$得答案.
解答 解:∵z=$\frac{2-{i}^{2017}}{1+i}$=$\frac{2-({i}^{4})^{504}•i}{1+i}=\frac{2-i}{1+i}=\frac{(2-i)(1-i)}{(1+i)(1-i)}$=$\frac{1-3i}{2}$=$\frac{1}{2}-\frac{3}{2}i$,
∴$\overline{z}=\frac{1}{2}+\frac{3}{2}i$,
∴z的共轭复数在复平面内对应的点的坐标为($\frac{1}{2},\frac{3}{2}$),位于第一象限.
故选:A.
点评 本题考查复数代数形式的乘除运算,考查复数的代数表示法及其几何意义,是基础题.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:选择题
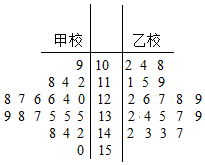
 一次数学考试后,某老师从自己所带的两个班级中各抽取6人,记录他们的考试成绩,得到如图所示的茎叶图.已知甲班6名同学成绩的平均数为82,乙班6名同学成绩的中位数为77,则x-y=( )
一次数学考试后,某老师从自己所带的两个班级中各抽取6人,记录他们的考试成绩,得到如图所示的茎叶图.已知甲班6名同学成绩的平均数为82,乙班6名同学成绩的中位数为77,则x-y=( )| A. | 3 | B. | -3 | C. | 4 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某市在对高三学生的4月理科数学调研测试的数据统计显示,全市10000名学生的成绩服从正态分布X~N(110,144),现从甲校100分以上的200份试卷中用系统抽样的方法抽取了20份试卷来分析,统计如下:
某市在对高三学生的4月理科数学调研测试的数据统计显示,全市10000名学生的成绩服从正态分布X~N(110,144),现从甲校100分以上的200份试卷中用系统抽样的方法抽取了20份试卷来分析,统计如下:| 试卷编号 | n1 | n2 | n3 | n4 | n5 | n6 | n7 | n8 | n9 | n10 |
| 试卷得分 | 109 | 118 | 112 | 114 | 126 | 128 | 127 | 124 | 126 | 120 |
| 试卷编号 | n11 | n12 | n13 | n14 | n15 | n16 | n17 | n18 | n19 | n20 |
| 试卷得分 | 135 | 138 | 135 | 137 | 135 | 139 | 142 | 144 | 148 | 150 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若事件A与事件B互斥,则事件A与事件B对立 | |
| B. | 函数y=$\sqrt{{x}^{2}+9}+\frac{1}{\sqrt{{x}^{2}+9}}$(x∈R)的最小值为2 | |
| C. | 若直线(m+1)x+my-2=0与直线mx-2y+5=0互相垂直,则m=1 | |
| D. | “p∧q为真命题”是“p∨q为真命题”的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x<1} | B. | {x|-2≤x≤2} | C. | {x|1<x≤2} | D. | {x|x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{4}$,$\frac{π}{3}$) | B. | ($\frac{π}{3}$,$\frac{2π}{3}$) | C. | ($\frac{2π}{3}$,$\frac{5π}{6}$) | D. | (0,$\frac{π}{3}$)∪($\frac{3π}{4}$,π) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com