练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．已知|$\overrightarrow{a}$|2=1，|$\overrightarrow{b}$|2=2，（$\overrightarrow{a}$-$\overrightarrow{b}$）•$\overrightarrow{a}$=0，则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为（　　）
    A．30°B．45°C．60°D．90°

    分析 设$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ，则由题意求得$\overrightarrow{a}$•$\overrightarrow{b}$=${\overrightarrow{a}}^{2}$=0，再利用两个向量的数量积的定义求得cosθ的值，可得θ的值．

    解答 解：∵已知|$\overrightarrow{a}$|2=1，|$\overrightarrow{b}$|2=2，（$\overrightarrow{a}$-$\overrightarrow{b}$）•$\overrightarrow{a}$=0，∴${\overrightarrow{a}}^{2}$-$\overrightarrow{a}•\overrightarrow{b}$=0，
    设$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ，则$\overrightarrow{a}$•$\overrightarrow{b}$=${\overrightarrow{a}}^{2}$=1•$\sqrt{2}$•cosθ，求得cosθ=$\frac{\sqrt{2}}{2}$，∴θ=45°，
    故选：B．

    点评 本题主要考查两个向量的数量积的定义，求两个向量的夹角，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    15．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的图象与x轴的一个交点$（-\frac{π}{12}，0）$到其相邻的一条对称轴的距离为$\frac{π}{4}$．若$f（\frac{π}{12}）=\frac{3}{2}$，则函数f（x）在$[0，\frac{π}{2}]$上的最小值为（　　）
    A．$\frac{1}{2}$B．$-\sqrt{3}$C．$-\frac{{\sqrt{3}}}{2}$D．$-\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．设函数$y=sin（{ωx+\frac{π}{3}}）$（0＜x＜π），当且仅当$x=\frac{π}{12}$时，y取得最大值，则正数ω的值为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．某工厂为了了解一批产品的净重（单位：克）情况，从中随机抽测了200件产品的净重，所得数据均在区间[96，106]上，其频率分布直方图如图所示，已知各个小方形按高度依次构成一个等差数列，则在抽测的200件产品中，净重在区间[98，102）上的产品件数是100．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

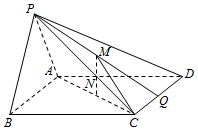    20．如图，在四棱锥P-ABCD中，平面PAB⊥底面ABCD，其中PA=PB，四边形ABCD是菱形，N为AC的中点，M是△PCD的中线PQ的中点．
    （Ⅰ）证明：MN∥平面PAB；
    （Ⅱ）证明：平面MNC⊥平面ABCD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．F1，F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a，b＞0）的左右焦点，点P在双曲线上，满足$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=0，若△PF1F2的内切圆半径与外接圆半径之比为$\frac{\sqrt{3}-1}{2}$，则该双曲线的离心率为（　　）
    A．$\sqrt{2}$B．$\sqrt{3}$C．$\sqrt{2}$+1D．$\sqrt{3}$+1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知在直角坐标系xOy中，圆C的参数方程为$\left\{\begin{array}{l}{x=3+2cosθ}\\{y=-4+2sinθ}\end{array}\right.$（θ为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为ρcos（θ-$\frac{π}{4}$）=$\sqrt{2}$．求圆C的普通方程和直线l的直角坐标方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知平面上三个向量$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$，给出下列说法：
    ①若$\overrightarrow{c}$=$\overrightarrow{a}$$+\overrightarrow{b}$，则$\overrightarrow{a}$、$\overrightarrow{b}$可以作为基底；
    ②若$\overrightarrow{a}$$∥\overrightarrow{b}$，且|$\overrightarrow{a}$|=|$\overrightarrow{b}$|，则$\overrightarrow{a}$=$\overrightarrow{b}$；
    ③若$\overrightarrow{a}$=$λ\overrightarrow{b}$，则|$\overrightarrow{a}$|=λ|$\overrightarrow{b}$|；
    ④若$\overrightarrow{a}$$+\overrightarrow{b}+\overrightarrow{c}$=$\overrightarrow{0}$，则|$\overrightarrow{c}$|≤|$\overrightarrow{a}$|+|$\overrightarrow{b}$|．
    其中正确说法的序号是④（写出所有正确的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．在一次购物抽奖活动中，假设10张奖券中有一等奖奖券1张，可获价值50元的奖品，有二等奖奖券3张，每张可获价值10元的奖品，其余6张没有奖品．
    （1）顾客甲从10张奖券中任意抽取1张，求中奖金额X的分布列；
    （2）顾客乙从10张奖券中任意抽取2张，
    ①求顾客乙中奖的概率；
    ②设顾客乙获得的奖品总价值为Y元，求Y的分布列．

    查看答案和解析>>

    同步练习册答案