
分析 由题意轴截面为正方形 EFGH 的圆柱的体积为2π,正方形的边长为1.可以从E点沿圆柱的侧面到相对顶点G的最短距离为圆柱侧面展开图一个顶点到对边中点的距离,利用勾股定理就可以求出其值.
解答 解:轴截面为正方形 EFGH 的圆柱的体积为2π,正方形的边长为1
从E点沿圆柱的侧面到相对顶点G的最短距离即为圆柱侧面展开图一个顶点到对边中点的距离,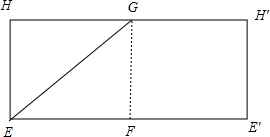
∵圆柱的轴截面的边长为1,
故GF=2,EF=π,
∴EG=$\sqrt{{π}^{2}+4}$,
故答案为:$\sqrt{{π}^{2}+4}$.
点评 本题考查的知识点是旋转体的展开图,其中将问题转化为平面上两点之间的距离线段最短是解答的关键.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
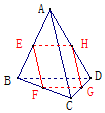 已知E,F,G,H分别是空间四边形四条边AB,BC,CD,DA的中点,
已知E,F,G,H分别是空间四边形四条边AB,BC,CD,DA的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1,2,3,4,5 | B. | 4,14,24,34,44 | C. | 2,4,6,8,10 | D. | 4,13,22,31,40 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2,3 | C. | 1,4 | D. | 1,2,3,4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
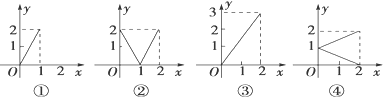
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com