Question

10．设集合M={x|0≤x≤2}，N={y|0≤y≤2}．下列四个图象中能表示从集合M到集合N的函数关系的有（　　）

• A． 0个
• B． 1个
• C． 2个
• D． 3个

Answer 1

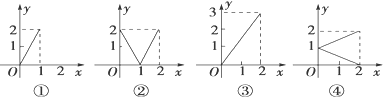
分析 根据函数的定义，对照各个图象可得：图①中集合M中属于区间（1，2]内的元素没有象，不符合题意；图④中集合M的一个元素对应N中的两个元素，也不符合题意；图②③都满足M中任意一个元素，N中有唯一元素与之对应，符合题意．

解答 解：由题意知：M={x|0≤x≤2}，N={y|0≤y≤3}，
对于图①中，在集合M中区间（1，2]内的元素没有象，比如f（1.5）的值就不存在，所以图①不符合题意；
对于图②中，对于M中任意一个元素，N中有唯一元素与之对应，符合函数的对应法则，故②正确；
对于图③中，对于M中任意一个元素，N中有唯一元素与之对应，且这种对应是一一对应，故③正确；
对于图④中，集合M的一个元素对应N中的两个元素．比如当x=1时，有两个y值与之对应，不符合函数的定义，故④不正确
故选：B．

点评 本题考查的是函数的概念和函数图象的综合类问题．在解答时充分体现了函数概念的知识、函数图象的知识以及问题转化的思想，属于中档题．