
【题目】将数字“![]() ”重新排列后得到不同的偶数个数为( )
”重新排列后得到不同的偶数个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】分析:根据题意,按偶数的个位数字分3种情况讨论,①,个位数字为0,②,个位数字为2,③,个位数字为4,分别求出每种情况下偶数的数目,由加法原理计算可得答案.
详解:根据题意,分3种情况讨论:
①,个位数字为0,在前面5个数位中任选2个,安排2个数字4,有C52=10种情况,
将剩下的3个数字全排列,安排在其他的数位,有A33=6种情况,
则此时有10×6=60个偶数,
②,个位数字为2,0不能在首位,有4种情况,
在剩下的4个数位中任选2个,安排2个数字4,有C42=6种情况,
将剩下的2个数字全排列,安排在其他的数位,有A22=2种情况,
则此时有4×6×2=48个偶数,
③,个位数字为4,0不能在首位,有4种情况,
将剩下的4个数字全排列,安排在其他的数位,有A44=24种情况,
则此时有4×24=96个偶数,
则有60+48+96=204个偶数;
故选:C.


科目:高中数学 来源: 题型:
【题目】一个口袋里装有![]() 个白球和
个白球和![]() 个红球,从口袋中任取
个红球,从口袋中任取![]() 个球.
个球.
(1)共有多少种不同的取法?
(2)其中恰有一个红球,共有多少种不同的取法?
(3)其中不含红球,共有多少种不同的取法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】夏天喝冷饮料已成为年轻人的时尚. 某饮品店购进某种品牌冷饮料若干瓶,再保鲜.
(Ⅰ)饮品成本由进价成本和可变成本(运输、保鲜等其它费用)组成.根据统计,“可变成本”![]() (元)与饮品数量
(元)与饮品数量![]() (瓶)有关系.
(瓶)有关系.![]() 与
与![]() 之间对应数据如下表:
之间对应数据如下表:
饮品数量 | 2 | 4 | 5 | 6 | 8 |
可变成本 | 3 | 4 | 4 | 4 | 5 |
依据表中的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;如果该店购入20瓶该品牌冷饮料,估计“可变成本”约为多少元?
;如果该店购入20瓶该品牌冷饮料,估计“可变成本”约为多少元?
(Ⅱ)该饮品店以每瓶10元的价格购入该品牌冷饮料若干瓶,再以每瓶15元的价格卖给顾客。如果当天前8小时卖不完,则通过促销以每瓶5元的价格卖给顾客(根据经验,当天能够把剩余冷饮料都低价处理完毕,且处理完毕后,当天不再购进).该店统计了去年同期100天该饮料在每天的前8小时内的销售量(单位:瓶),制成如下表:
每日前8个小时 销售量(单位:瓶) | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
频数 | 10 | 15 | 16 | 16 | 15 | 13 | 15 |
若以100天记录的频率作为每日前8小时销售量发生的概率,若当天购进18瓶,求当天利润的期望值.
(注:利润=销售额![]() 购入成本
购入成本![]() “可变本成”)
“可变本成”)
参考公式:回归直线方程为![]() ,其中
,其中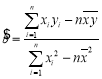
参考数据:![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】人造地球卫星绕地球运行遵循开普勒行星运动定律:卫星在以地球为焦点的椭圆轨道上绕地球运行时,其运行速度是变化的,速度的变化服从面积守恒规律,即卫星的向径(卫星至地球的连线)在相同的时间内扫过的面积相等.设椭圆的长轴长、焦距分别为![]() 李明根据所学的椭圆知识,得到下列结论:
李明根据所学的椭圆知识,得到下列结论:

①卫星向径的最小值为![]() ,最大值为
,最大值为![]() ;
;
②卫星向径的最小值与最大值的比值越小,椭圆轨道越扁;
③卫星运行速度在近地点时最小,在远地点时最大
其中正确结论的个数是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,
中,![]() ,不在
,不在![]() 轴上的动点
轴上的动点![]() 满足
满足![]() 于点
于点![]() 为
为![]() 的中点。
的中点。
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设曲线![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,斜率为
,斜率为![]() 的直线交
的直线交![]() 于
于![]() 两点,记直线
两点,记直线![]() 的斜率分别为
的斜率分别为![]() ,试问
,试问![]() 是否为定值?若是,求出该定值;若不是,请说明理由。
是否为定值?若是,求出该定值;若不是,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》节目组决定把《将进酒》、《山居秋暝》、《望岳》、《送杜少府之任蜀州》和另外确定的两首诗词排在后六场,并要求《将进酒》与《望岳》相邻,且《将进酒》排在《望岳》的前面,《山居秋暝》与《送杜少府之任蜀州》不相邻,且均不排在最后,则后六场开场诗词的排法有_____________种.(用数字作答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com