
分析 (Ⅰ)设等差数列{an}的公差为d,则由已知条件列式求得首项和公差,代入等差数列的通项公式得答案;
(Ⅱ)求出${b}_{1}=1,{b}_{4}={a}_{15}=\frac{15+1}{2}=8$,再求出等比数列的公比,由等比数列的前n项和公式求得{bn}前n项和Tn.
解答 解:(Ⅰ)设等差数列{an}的公差为d,则由已知条件得:
$\left\{\begin{array}{l}{{a}_{1}+2d=2}\\{3{a}_{1}+\frac{3×2}{2}d=\frac{9}{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}_{1}=1}\\{d=\frac{1}{2}}\end{array}\right.$.
代入等差数列的通项公式得:${a}_{n}=1+\frac{n-1}{2}=\frac{n+1}{2}$;
(Ⅱ)由(Ⅰ)得,${b}_{1}=1,{b}_{4}={a}_{15}=\frac{15+1}{2}=8$.
设{bn}的公比为q,则${q}^{3}=\frac{{b}_{4}}{{b}_{1}}=8$,从而q=2,
故{bn}的前n项和${T}_{n}=\frac{{b}_{1}(1-{q}^{n})}{1-q}=\frac{1×(1-{2}^{n})}{1-2}={2}^{n}-1$.
点评 本题考查了等差数列和等比数列的通项公式,考查了等差数列和等比数列的前n项和,是中档题.


科目:高中数学 来源: 题型:选择题

| A. | 逐年比较,2008年减少二氧化硫排放量的效果最显著 | |
| B. | 2007年我国治理二氧化硫排放显现成效 | |
| C. | 2006年以来我国二氧化硫年排放量呈减少趋势 | |
| D. | 2006年以来我国二氧化硫年排放量与年份正相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | s≤$\frac{3}{4}$ | B. | s≤$\frac{5}{6}$ | C. | s≤$\frac{11}{12}$ | D. | s≤$\frac{25}{24}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,1] | B. | (-3,1) | C. | (-∞,-3]∪[1,+∞) | D. | (-∞,-3)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
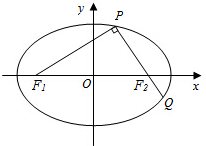 如题图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为F1,F2,且过F2的直线交椭圆于P,Q两点,且PQ⊥PF1.
如题图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为F1,F2,且过F2的直线交椭圆于P,Q两点,且PQ⊥PF1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com