
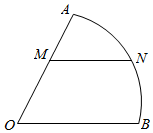
 如图,扇形AOB是某个旅游景点的平面示意图,圆心角AOB的大小等于$\frac{π}{3}$,半径OA=200m,点M在半径OA上,点N在$\widehat{AB}$上,且MN∥OB,求观光道路OM与MN长度之和的最大值.
如图,扇形AOB是某个旅游景点的平面示意图,圆心角AOB的大小等于$\frac{π}{3}$,半径OA=200m,点M在半径OA上,点N在$\widehat{AB}$上,且MN∥OB,求观光道路OM与MN长度之和的最大值. 分析 连接ON,设∠MON=θ,则0<θ<$\frac{π}{3}$,在△MON中由正弦定理可得MN=$\frac{400}{\sqrt{3}}$sin θ,OM=$\frac{400}{\sqrt{3}}$sin($\frac{π}{3}$-θ),化简MN+OM由三角函数的最值可得.
解答 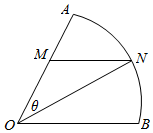 解:连接ON,设∠MON=θ,则0<θ<$\frac{π}{3}$,
解:连接ON,设∠MON=θ,则0<θ<$\frac{π}{3}$,
在△MON中,ON=200,∠OMN=$\frac{2π}{3}$,
由正弦定理可得$\frac{200}{sin\frac{2π}{3}}$=$\frac{MN}{sinθ}$=$\frac{OM}{sin(\frac{π}{3}-θ)}$,
∴MN=$\frac{400}{\sqrt{3}}$sinθ,OM=$\frac{400}{\sqrt{3}}$sin($\frac{π}{3}$-θ),
∴MN+OM=$\frac{400}{\sqrt{3}}$[sin θ+sin($\frac{π}{3}$-θ)]
=$\frac{400}{\sqrt{3}}$( sin θ+$\frac{\sqrt{3}}{2}$cos θ-$\frac{1}{2}$sin θ)=$\frac{400}{\sqrt{3}}$sin($\frac{π}{3}$+θ),
∵0<θ<$\frac{π}{3}$,∴$\frac{π}{3}$<$\frac{π}{3}$+θ<$\frac{2π}{3}$,
∴当θ=$\frac{π}{6}$时,sin($\frac{π}{3}$+θ)=1 最大,MN+OM最大,
其最大值是$\frac{400}{3}$$\sqrt{3}$m.
点评 本题考查弧度制和正弦定理以及三角函数的最值,属中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | s≤$\frac{3}{4}$ | B. | s≤$\frac{5}{6}$ | C. | s≤$\frac{11}{12}$ | D. | s≤$\frac{15}{24}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
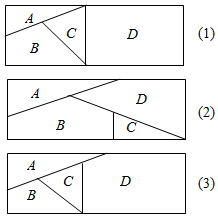 用n(n∈N*)种不同颜色给如图的4个区域涂色,要求相邻区域不能用同一种颜色.
用n(n∈N*)种不同颜色给如图的4个区域涂色,要求相邻区域不能用同一种颜色.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com