
分析 由已知得f(x+6)=$\frac{1}{f(x+3)}$=f(x),从而f(2017)=f(336×6+1)=f(1)=f(-2+3)=$\frac{1}{f(-2)}$,由此能求出结果.
解答 解:∵函数f(x)满足f(x+3)=$\frac{1}{f(x)}$,
∴f(x+6)=$\frac{1}{f(x+3)}$=f(x),
∵f(-2)=2,
∴f(2017)=f(336×6+1)=f(1)=f(-2+3)=$\frac{1}{f(-2)}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数的周期性的合理运用.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:解答题
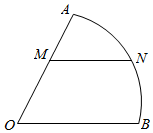 如图,扇形AOB是某个旅游景点的平面示意图,圆心角AOB的大小等于$\frac{π}{3}$,半径OA=200m,点M在半径OA上,点N在$\widehat{AB}$上,且MN∥OB,求观光道路OM与MN长度之和的最大值.
如图,扇形AOB是某个旅游景点的平面示意图,圆心角AOB的大小等于$\frac{π}{3}$,半径OA=200m,点M在半径OA上,点N在$\widehat{AB}$上,且MN∥OB,求观光道路OM与MN长度之和的最大值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com