
分析 ①根据三角函数的诱导公式以及函数奇偶性的定义进行判断,
②根据平面向量数量积的应用进行判断,
③根据象限角和正切值的关系进行判断,
④根据三角函数的对称性进行判断,
⑤根据三角函数的对称性进行判断.
解答 解:①函数y=cos($\frac{2}{3}$x+$\frac{π}{2}$)=-sin$\frac{2}{3}$x是奇函数,故①正确;
②在△ABC中,若$\overrightarrow{AB}•\overrightarrow{BC}>0$,则AB•BCcos(π-B)=-AB•BCcosB>0,则cosB<0,则B是钝角,则△ABC为钝角三角形;故②正确,
③若α,β是第一象限角,当α=$\frac{π}{4}$,β=$\frac{π}{4}$+2π,满足α<β,但tanα=tanβ;故③错误,
④由2x+$\frac{5π}{4}$=kπ+$\frac{π}{2}$,得x=$\frac{kπ}{2}$-$\frac{3π}{8}$,k∈Z,
则当k=1时,$x=\frac{π}{8}$,则$x=\frac{π}{8}$是函数$y=sin({2x+\frac{5π}{4}})$的一条对称轴,故④正确;
⑤由2x+$\frac{π}{3}$=kπ,则x=$\frac{kπ}{2}$-$\frac{π}{6}$,则函数的对称中心为($\frac{kπ}{2}$-$\frac{π}{6}$,0),
由$\frac{kπ}{2}$-$\frac{π}{6}$=$\frac{π}{12}$得k=$\frac{1}{2}$不是整数,不满足条件.故函数$y=sin({2x+\frac{π}{3}})$的图象关于点($\frac{π}{12}$,0)成中心对称错误,故⑤错误,
故答案为:①②④
点评 本题主要考查命题的真假判断,涉及三角函数的图象和性质,综合性较强,考查学生的运算和推理能力,难度不大.


科目:高中数学 来源: 题型:选择题
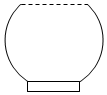 一个高为H容积为V的鱼缸的轴截面如图所示.现向空鱼缸内注水,直到注满为止.当鱼缸水深为h时,水的体积记为v.函数v=f(h)的大致图象可能是( )
一个高为H容积为V的鱼缸的轴截面如图所示.现向空鱼缸内注水,直到注满为止.当鱼缸水深为h时,水的体积记为v.函数v=f(h)的大致图象可能是( )| A. | 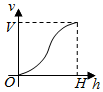 | B. | 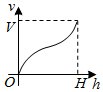 | C. | 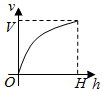 | D. | 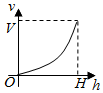 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x<1} | B. | {x|0≤x<2} | C. | {x|0≤x≤1} | D. | {x|0≤x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
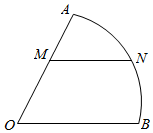 如图,扇形AOB是某个旅游景点的平面示意图,圆心角AOB的大小等于$\frac{π}{3}$,半径OA=200m,点M在半径OA上,点N在$\widehat{AB}$上,且MN∥OB,求观光道路OM与MN长度之和的最大值.
如图,扇形AOB是某个旅游景点的平面示意图,圆心角AOB的大小等于$\frac{π}{3}$,半径OA=200m,点M在半径OA上,点N在$\widehat{AB}$上,且MN∥OB,求观光道路OM与MN长度之和的最大值.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com