
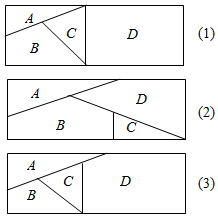
 用n(n∈N*)种不同颜色给如图的4个区域涂色,要求相邻区域不能用同一种颜色.
用n(n∈N*)种不同颜色给如图的4个区域涂色,要求相邻区域不能用同一种颜色.分析 (1)如图(1)据题意,分四个步骤来完成,由乘法原理计算可得答案.
图(2)分两类,若A,C相同,若A,C不同,根据分类计数原理可得.
(2)A有n种方法,B有n-1种方法,C有n-2种方法,D有n-2种方法,共有涂色方法n(n-1)(n-2)(n-2)=180,计算可得答案.
解答 解:(1)当n=6时,图(1)A有6种方法,B有5种方法,C有4种方法,D有5种方法,共有涂色方法6×5×4×5=600种
图(2)若A,C相同,则A有6种方法,B有5种方法,D有4种方法,共有6×5×4=120种
若A,C不同,则A有6种方法,B有5种方法,C有4种方法,D有3种方法,共有6×5×4×3=360种
∴共有涂色方法120+360=480种.
(2)A有n种方法,B有n-1种方法,C有n-2种方法,D有n-2种方法,共有涂色方法n(n-1)(n-2)(n-2)种
由n(n-1)(n-2)(n-2)=180
解得n=5
点评 本题考查涂色问题,是排列、组合的典型题目,一般涉及分类加法原理与分步乘法原理,注意认真分析题意,把握好限制条件.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 命中环数 | 10环 | 9环 | 8环 |
| 概 率 | 0.12 | 0.18 | 0.28 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
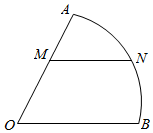 如图,扇形AOB是某个旅游景点的平面示意图,圆心角AOB的大小等于$\frac{π}{3}$,半径OA=200m,点M在半径OA上,点N在$\widehat{AB}$上,且MN∥OB,求观光道路OM与MN长度之和的最大值.
如图,扇形AOB是某个旅游景点的平面示意图,圆心角AOB的大小等于$\frac{π}{3}$,半径OA=200m,点M在半径OA上,点N在$\widehat{AB}$上,且MN∥OB,求观光道路OM与MN长度之和的最大值.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com