
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
分析 根据条件求出函数的周期,利用函数的周期性将条件进行转化求解即可.
解答 解:由f(x)=-f(x+$\frac{3}{2}$),得f(x+$\frac{3}{2}$)=-f(x),
则f(x+3)=-f(x+$\frac{3}{2}$)=-[f(x)]=f(x),
则函数f(x)是周期为3的周期函数,
∵f(-2)=f(-1)=-1,f(0)=2,
∴f(-2+3)=f(-1+3)=-1,
即f(1)=f(2)=-1,f(3)=2,
则f(1)+f(2)+f(3)=-1-1+2=0,
则f(1)+f(2)+f(3)+…+f(2008)+f(2009)=669×[f(1)+f(2)+f(3)]+f(2008)+f(2009)
=f(2008)+f(2009)=f(1)+f(2)=-1-1=-2,
故选:A
点评 本题主要考查函数值的计算,根据条件求出函数的周期,利用函数的周期性进行转化是解决本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
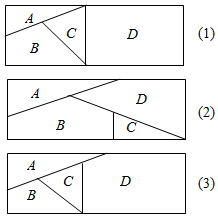 用n(n∈N*)种不同颜色给如图的4个区域涂色,要求相邻区域不能用同一种颜色.
用n(n∈N*)种不同颜色给如图的4个区域涂色,要求相邻区域不能用同一种颜色.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
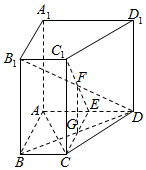 如图,在四棱柱ABCD-A1B1C1D1中,AC⊥B1D,BB1⊥底面ABCD,E为线段AD上的任意一点(不包括A、D两点),平面CEC1与平面BB1D交于FG.
如图,在四棱柱ABCD-A1B1C1D1中,AC⊥B1D,BB1⊥底面ABCD,E为线段AD上的任意一点(不包括A、D两点),平面CEC1与平面BB1D交于FG.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |z1|+|z2|>|z1+z2| | B. | |z1|-|z2|>|z1-z2| | C. | |z1|+|z2|≥|z1+z2| | D. | |z1|-|z2|≥|z1-z2| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com