
分析 (I)根据线性规划原理,可得z的最大值zn=2n,从而得到Sn=2n-an.运用数列前n项和Sn与an的关系,算出2an=an-1+2,由此代入数列{an-2}再化简整理,即可得到{an-2}是以-1为首项,公比q=$\frac{1}{2}$的等比数列;
(II)由(I)结合等比数列通项公式,得出an=2-($\frac{1}{2}$)n-1,从而得到Sn=2n-2+($\frac{1}{2}$)n-1,结合等差数列和等比数列的求和公式,即可算出{Sn}的前n项和Tn的表达式.
解答 解:(Ⅰ)∵目标函数对应直线:z=x+y,
区域$\left\{{\begin{array}{l}{x+2y≤2n}\\{x≥0}\\{y≥0}\end{array}}\right.$,(n∈N*),表示以x轴、y轴和直线x+2y=2n为三边的三角形,
∴当x=2n,y=0时,z的最大值zn=2n
∵(Sn,an)在直线zn=x+y上
∴zn=Sn+an,可得Sn=2n-an,
当n≥2时,可得an=Sn-Sn-1=(2n-an)-[2(n-1)-an-1]
化简整理,得2an=an-1+2
因此,an-2=$\frac{1}{2}$(an-1+2)-2=$\frac{1}{2}$(an-1-2)
当n=1时,an-2=a1-2=-1
∴数列{an-2}是以-1为首项,公比q=$\frac{1}{2}$的等比数列,
得an-2=-($\frac{1}{2}$)n-1,
∴an=2-($\frac{1}{2}$)n-1;
(II)bn=nan,bn=2n-n($\frac{1}{2}$)n-1;
设:An=n($\frac{1}{2}$)n-1,前n项和Mn,
Mn=1×${(\frac{1}{2})}^{0}$+2×$({\frac{1}{2})}^{1}$+3$(\frac{1}{2})^{2}$+…+n($\frac{1}{2}$)n-1,
∴$\frac{1}{2}$Mn=1×$\frac{1}{2}$+2×$(\frac{1}{2})^{2}$+3×$(\frac{1}{2})^{3}$+…+n($\frac{1}{2}$)n,
两式相减:$\frac{1}{2}$Mn=1+$\frac{1}{2}$+$(\frac{1}{2})^{2}$+$(\frac{1}{2})^{3}$+…+($\frac{1}{2}$)n-1-n($\frac{1}{2}$)n,
∴Mn=4-(n+2)×($\frac{1}{2}$)n-1,
∴Tn=2×$\frac{n(n+1)}{2}$-4+(n+2)×($\frac{1}{2}$)n-1,
=n2+n-4+(n+2)×($\frac{1}{2}$)n-1.
Mn=n2+n-4+(n+2)×($\frac{1}{2}$)n-1.
点评 本题给出数列和线性规划相综合的问题,求数列的通项和前n项和,着重考查了等差数列、等比数列的通项公式,数列的求和与简单线性规划等知识,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
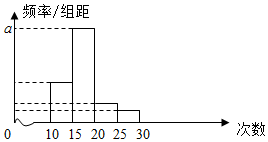 对某校高二学生参加舍去服务次数进行统计.随机抽取M名学生作为样本,得到这M名学生参加舍去服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如下:
对某校高二学生参加舍去服务次数进行统计.随机抽取M名学生作为样本,得到这M名学生参加舍去服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如下:| 分组 | 频数 | 频率 |
| [10,15) | 10 | 0.25 |
| [15,20) | 25 | n |
| [20,25) | m | p |
| [25,30) | 2 | 0.05 |
| 合计 | M | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{3}{4}$]∪[$\frac{3}{2}$,+∞) | B. | (0,$\frac{3}{4}]$ | C. | [$\frac{3}{2}$,+∞) | D. | [$\frac{3}{4},\frac{3}{2}]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com