
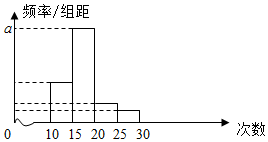
 对某校高二学生参加舍去服务次数进行统计.随机抽取M名学生作为样本,得到这M名学生参加舍去服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如下:
对某校高二学生参加舍去服务次数进行统计.随机抽取M名学生作为样本,得到这M名学生参加舍去服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如下:| 分组 | 频数 | 频率 |
| [10,15) | 10 | 0.25 |
| [15,20) | 25 | n |
| [20,25) | m | p |
| [25,30) | 2 | 0.05 |
| 合计 | M | 1 |
分析 (1)根据频率,频数的关系以即可求出答案;
(2)众数即频率最高组的组中,平均数是各组组中与频率积的累加积,而中位数能把频率分布直方图面积平均分配.
解答 解:(1)由分组[10,15)内的频数是10,频率是0.25知,M=$\frac{10}{0.25}$,
∴M=40.
∴10+25+m+2=40,m=3,
∴n=$\frac{25}{40}$=$\frac{5}{8}$=0.625,
p=$\frac{3}{40}$=0.075
∵a是对应分组[15,20)的频率与组距的商,所以$\frac{0.625}{5}$=0.125,
(2)∵第一组的频率为0.25,第二组的频率为0.625
故估计这次学生参加社区服务人数的中位数为15+$\frac{0.25}{0.625}$×5=17,
故估计这次学生参加社区服务人数的平均数为12.5×0.25+17.5×0.625+22.5×0.075+27.5×0.05=17.125.
点评 本题考查的知识点是频率分布直方图,熟练掌握频率=$\frac{频数}{样本容量}$,矩形的高=$\frac{频率}{组距}$等常用公式及利用直方图计算平均数、中位数的方法是解答的关键


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:选择题
| A. | |z1|+|z2|>|z1+z2| | B. | |z1|-|z2|>|z1-z2| | C. | |z1|+|z2|≥|z1+z2| | D. | |z1|-|z2|≥|z1-z2| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
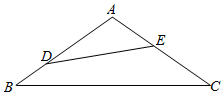 某小区要将如图所示的一块三角形边角地修建成花圃.根据建造规划,要求横穿花圃的直线灌溉水道DE恰好把花圃分成面积相等的两部分(其中D在边AB上,E在边AC上)已知AB=AC=2a,∠BAC=120°
某小区要将如图所示的一块三角形边角地修建成花圃.根据建造规划,要求横穿花圃的直线灌溉水道DE恰好把花圃分成面积相等的两部分(其中D在边AB上,E在边AC上)已知AB=AC=2a,∠BAC=120°查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com