
| A. | (0,$\frac{3}{4}$]∪[$\frac{3}{2}$,+∞) | B. | (0,$\frac{3}{4}]$ | C. | [$\frac{3}{2}$,+∞) | D. | [$\frac{3}{4},\frac{3}{2}]$ |
分析 先将f(x)的单调性分析出,找到极大极小值,由此找到f(x1)和f(x2)的值域,等价转换为两集合的包含关系,再分类讨论即可.
解答 解:∵f(x)=x2-$\frac{2}{3}$ ax3(a>0),
∴f′(x)=2x-2ax2,
则由f′(x)>0得到函数f(x)的增区间为(0,$\frac{1}{a}$) 减区间为(-∞,0)、($\frac{1}{a}$,+∞),
则f(x)极小值=f(0)=0,f(x)极大值=f($\frac{1}{a}$)=$\frac{1}{3{a}^{2}}$,
由此可知f(x)的图象,
设集合M={f(x)|x∈(2,+∞)},N={$\frac{1}{f(x)}$|x∈(1,+∞)},
则对任意x1∈(2,+∞),都存在x2∈(1,+∞)
使得f(x1)f(x2)=l,
等价于M⊆N,显然0∉N.
①当$\frac{3}{2a}$>2,即0<a<$\frac{3}{4}$时,0∈M,不满足M⊆N;
②当1≤$\frac{3}{2a}$≤2,即$\frac{3}{4}$≤a≤$\frac{3}{2}$时,f(x)≤0,M=(-∞,f(2))⊆(-∞,0),
由于f(1)=$\frac{3-2a}{3}$≥0,有f(x)在(1,+∞)上的取值范围包含在(-∞,0)内满足M⊆N;
③当$\frac{3}{2a}$<1,即a>$\frac{3}{2}$,有f(1)<0,f(x)在(1,+∞)上单减,
∴B=($\frac{1}{f(x)}$,0),A=(0,f(2))不满足M⊆N,
综上可知a∈[$\frac{3}{4}$,$\frac{3}{2}$],
故选D.
点评 本题考查由导函数寻找f(x)的极大极小值,由此找到f(x1)和f(x2)的值域,等价转换为两集合的包含关系,再分类讨论即可.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
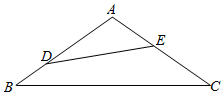 某小区要将如图所示的一块三角形边角地修建成花圃.根据建造规划,要求横穿花圃的直线灌溉水道DE恰好把花圃分成面积相等的两部分(其中D在边AB上,E在边AC上)已知AB=AC=2a,∠BAC=120°
某小区要将如图所示的一块三角形边角地修建成花圃.根据建造规划,要求横穿花圃的直线灌溉水道DE恰好把花圃分成面积相等的两部分(其中D在边AB上,E在边AC上)已知AB=AC=2a,∠BAC=120°查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com