练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．根据如图所示的流程图，若输入值x∈[0，3]，则输出值y的取值范围是[1，7]．

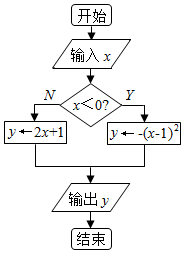
    分析 根据程序框图知：算法的功能是求y=$\left\{\begin{array}{l}{-（x-1）^{2}}&{x＜0}\\{2x+1}&{x≥0}\end{array}\right.$的值，求分段函数的值域可得答案．

    解答 解：由程序框图知：算法的功能是求y=$\left\{\begin{array}{l}{-（x-1）^{2}}&{x＜0}\\{2x+1}&{x≥0}\end{array}\right.$的值，
    当x∈[0，3]时，满足条件x≥0，函数y=2x+1∈[1，7]．
    故答案为：[1，7]．

    点评 本题考查了选择结构的程序框图，分段函数求值域的方法是先在不同的段上值域，再求并集，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    3．若cos（$\frac{π}{6}$-α）=$\frac{3}{5}$，则cos（$\frac{5π}{6}$+α）的值是（　　）
    A．$\frac{3}{5}$B．-$\frac{3}{5}$C．$\frac{4}{5}$D．-$\frac{4}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知x与y满足$\left\{{\begin{array}{l}{x+y≤2}\\{x≥0}\\{y≥0}\end{array}}\right.$，则y-x的最大值为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．若命题“?x0∈R，x02-3ax0+9＜0”为假命题，则实数a的取值范围是[-2，2]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．（Ⅰ）化简$\frac{sin（2π-α）tan（α+π）tan（-α）}{cos（π-α）tan（3π-α）}$．
    （Ⅱ）计算$cos\frac{25π}{6}+cos\frac{25π}{3}+tan（{-\frac{25π}{4}}）+sin\frac{5π}{6}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

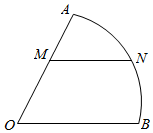    18．如图，扇形AOB是某个旅游景点的平面示意图，圆心角AOB的大小等于$\frac{π}{3}$，半径OA=200m，点M在半径OA上，点N在$\widehat{AB}$上，且MN∥OB，求观光道路OM与MN长度之和的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知实数a＞0，b＞0
    （1）若a+b＞2，求证：$\frac{1+b}{a}，\frac{1+a}{b}$中至少有一个小于2；
    （2）若a-b=2，求证：a3+b＞8；
    （3）若a2-b2=2，求证：a（3a-2b）≥4$\sqrt{2}$+6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．在△ABC中，
    （1）已知$\sqrt{2}$a=2bsinA，求B；
    （2）已知a2+b2+$\sqrt{2}$ab=c2，求C．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．在三角形ABC中AB=a，AC=b（b＞0，a＞0），P是三角形ABC的外心，数量积$\overrightarrow{AP}$$•\overrightarrow{BC}$等于（　　）
    A．$\frac{a+b}{2}$B．a+bC．$\frac{{a}^{2}-{b}^{2}}{2}$D．$\frac{{b}^{2}-{a}^{2}}{2}$

    查看答案和解析>>

    同步练习册答案