
分析 (1)利用诱导公式,同角三角函数基本关系式化简即可得解;
(2)利用诱导公式,特殊角的三角函数值即可化简求值得解.
解答 本大题共2个小题,每小题5分,共10分
解:(1)原式=$\frac{sin(-α)tanαtan(-α)}{-cosα(-tanα)}$…(2分)
=$\frac{-sinαtanα(-tanα)}{cosαtanα}$…(3分)
=tanαtanα
=tan2α.…(5分)
(2)$cos\frac{25π}{6}+cos\frac{25π}{3}+tan({-\frac{25π}{4}})+sin\frac{5π}{6}$
$\begin{array}{l}=cos(4π+\frac{π}{6})+cos(8π+\frac{π}{3})+tan(-6π-\frac{π}{4})+\frac{1}{2}…(7分)\\=cos\frac{π}{6}+cos\frac{π}{3}+tan(-\frac{π}{4})+\frac{1}{2}…(8分)\\=\frac{{\sqrt{3}}}{2}+\frac{1}{2}-1+\frac{1}{2}=\frac{{\sqrt{3}}}{2}…(10分)\end{array}$
点评 本题主要考查了诱导公式,同角三角函数基本关系式,特殊角的三角函数值在三角函数化简求值中的应用,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12x-5y+30=0 | B. | 12x+5y-30=0 | ||
| C. | x=0或12x-5y+30=0 | D. | x=0或12x+5y-30=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
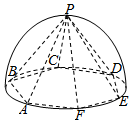 如图,半径为2的半球内有一内接正六棱锥P-ABCDEF(底面正六边形ABCDEF的中心为球心).求:正六棱锥P-ABCDEF的体积和侧面积.
如图,半径为2的半球内有一内接正六棱锥P-ABCDEF(底面正六边形ABCDEF的中心为球心).求:正六棱锥P-ABCDEF的体积和侧面积.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$R | B. | $\frac{1}{3}$πR | C. | $\frac{1}{2}$πR | D. | $\frac{2}{3}$πR |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com