练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数y＝sin(πx＋φ)(φ>0)的部分图象如图所示，设P是图象的最高点，A、B是图象与x轴的交点，则tan∠APB＝(　　)

    A．10                                                           B．8

    C.                                                             D.


    B

    [分析]　利用正弦函数的周期、最值等性质求解．

    [解析]　


    如图，过P作PC⊥x轴，垂足为C，设∠APC＝α，∠BPC＝β，∴∠APB＝α＋β，y＝sin(πx＋φ)，T＝＝2，tanα＝＝＝，tanβ＝＝＝，则tan(α＋β)＝＝＝8，

    ∴选B.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


     已知函数f (x)是正比例函数,函数g(x)是反比例函数,且f(1)=1,g(1)=1.

    (1) 求函数f(x),g(x)的解析式;

    (2) 判断函数h(x)=f(x)+g(x)的奇偶性;

    (3) 求证:函数S(x)=xf(x)+g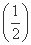在(0,+∞)上是单调增函数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知α为第二象限角，sinα＋cosα＝，则cos2α＝(　　)

    A．－                                                     B．－

    C.                                                           D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝2cos2x－sin2x(x∈R)的最小正周期和最大值分别为 (　　)

    A．2π，3                                                      B．2π，1

    C．π，3                                                        D．π，1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    给出下列命题：

    ①存在实数x，使得sinx＋cosx＝；②若α、β为第一象限角，且α>β，则tanα>tanβ；③函数y＝sin的最小正周期为5π；④函数y＝cos是奇函数；⑤函数y＝sin2x的图象向左平移个单位，得到y＝sin(2x＋)的图象．

    其中正确命题的序号是________(把你认为正确的序号都填上)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a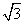＝(，cosx)，b＝(cos2x，sinx)，函数f(x)＝a·b－.

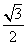    (1)求函数f(x)的单调递增区间；

    (2)若x∈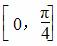，求函数f(x)的取值范围；

    (3)函数f(x)的图象经过怎样的平移可使其对应的函数成为奇函数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝－sin(2x＋)＋6sinxcosx－2cos2x＋1，x∈R.

    (1)求f(x)的最小正周期；

    (2)求f(x)在区间[0，]上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    命题：∀x∈[0，]，使3cos2＋sincos<a＋成立，则实数a的取值范围是(　　)

    A．(1，＋∞)                                                B．(，＋∞)

    C．(，＋∞)                                              D．(，＋∞)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


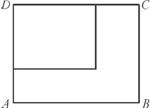
    现有一张长为80 cm、宽为60 cm的长方形铁皮ABCD,准备用它做成一只无盖长方体铁皮盒,要求材料利用率为100%,不考虑焊接处损失.如图,把长方形ABCD的一个角剪下一块正方形铁皮作为铁皮盒的底面,用余下材料剪拼后作为铁皮盒的侧面,设长方体的底面边长为x(cm),高为y(cm),体积为V(cm3).

    (1) 求出x与y的关系式;

     (2) 求该铁皮盒体积V的最大值.

    查看答案和解析>>

    同步练习册答案