
已知函数f (x)是正比例函数,函数g(x)是反比例函数,且f(1)=1,g(1)=1.
(1) 求函数f(x),g(x)的解析式;
(2) 判断函数h(x)=f(x)+g(x)的奇偶性;
(3) 求证:函数S(x)=xf(x)+g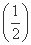 在(0,+∞)上是单调增函数.
在(0,+∞)上是单调增函数.
(1) 设f(x)=k1x(k1≠0),g(x)= (k2≠0),
(k2≠0),
因为f(1)=1,g(1)=1,所以k1=1,k2=1.所以f(x)=x,g(x)=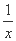 .
.
(2) 由(1)得h(x)=x+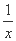 ,则函数h(x)的定义域是(-∞,0)∪(0,+∞),
,则函数h(x)的定义域是(-∞,0)∪(0,+∞),
h(-x)=-x+ =-
=-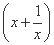 =-h(x),所以函数h(x)=f(x)+g(x)是奇函数.
=-h(x),所以函数h(x)=f(x)+g(x)是奇函数.
(3) 由(1)得S(x)=x2+2.设x1,x2∈(0,+∞),且x1<x2,
则S(x1)-S(x2)=(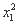 +2)-(
+2)-( +2)=
+2)=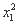 -
- =(x1-x2)(x1+x2).
=(x1-x2)(x1+x2).
因为x1,x2∈(0,+∞),且x1<x2,所以x1-x2<0,x1+x2>0,
所以S(x1)-S(x2)<0,所以S(x1)<S(x2).
所以函数S(x)= xf(x)+g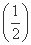 在(0,+∞)上是增函数.
在(0,+∞)上是增函数.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.已知函数f(x)=ax2+(b+1)x+(b-1)(a≠0).
(1)当a=1,b=-2时,求函数f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
里氏震级M的计算公式为:M=lgA-lgA0,其中A是测震仪记录的地震曲线的最大振幅,A0是相应的标准地震的振幅.假设在一次地震中,测震仪记录的最大振幅是1 000,此时标准地震的振幅为0.001,则此次地震的震级为________级;9级地震的最大振幅是5级地震最大振幅的________倍.
查看答案和解析>>
科目:高中数学 来源: 题型:
函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A、B是图象与x轴的交点,则tan∠APB=( )

A.10 B.8
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com