
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.已知函数f(x)=ax2+(b+1)x+(b-1)(a≠0).
(1)当a=1,b=-2时,求函数f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围.
 教学练新同步练习系列答案
教学练新同步练习系列答案科目:高中数学 来源: 题型:
若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“孪生函数”.那么函数的解析式为y=2x2+1,值域为{5,19,1}的“孪生函数”共有( )
A.4个 B.6个
C.8个 D.9个
查看答案和解析>>
科目:高中数学 来源: 题型:
已知f(x)=1-(x-a)(x-b)(a<b),m,n是f(x)的零点,且m<n,则实数a,b,m,n的大小关系是( )
A.m<a<b<n B.a<m<n<b
C.a<m<b<n D.m<a<n<b
查看答案和解析>>
科目:高中数学 来源: 题型:
某电信公司推出两种手机收费方式:A种方式是月租20元,B种方式是月租0元.一个月的本地网内打出电话时间t(分钟)与打出电话费s(元)的函数关系如图,当打出电话150分钟时,这两种方式电话费相差( )
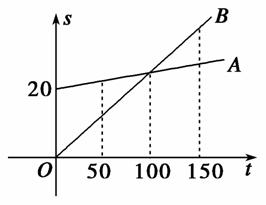
A.10元 B.20元
C.30元 D.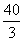 元
元
查看答案和解析>>
科目:高中数学 来源: 题型:
某工厂生产某种产品固定成本为2 000万元,并且每生产一单位产品,成本增加10万元,又知总收入k是单位产品数Q的函数,k(Q)=40Q-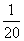 Q2,则总利润L(Q)的最大值是________万元.
Q2,则总利润L(Q)的最大值是________万元.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f (x)是正比例函数,函数g(x)是反比例函数,且f(1)=1,g(1)=1.
(1) 求函数f(x),g(x)的解析式;
(2) 判断函数h(x)=f(x)+g(x)的奇偶性;
(3) 求证:函数S(x)=xf(x)+g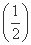 在(0,+∞)上是单调增函数.
在(0,+∞)上是单调增函数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com