
【题目】已知函数f(x)=( ![]() +
+ ![]() )x3(a>0,a≠1).
)x3(a>0,a≠1).
(1)讨论函数f(x)的奇偶性;
(2)求a的取值范围,使f(x)+f(2x)>0在其定义域上恒成立.
【答案】
(1)解:定义域为(﹣∞,0)∪(0,+∞),
∵f(﹣x)=( ![]() +
+ ![]() )(﹣x)3=﹣(
)(﹣x)3=﹣( ![]() +
+ ![]() )x3=(
)x3=( ![]() +
+ ![]() )=f(x)
)=f(x)
∴f(x)是偶函数.
(2)解:∵函数f(x)在定义域上是偶函数,
∴函数y=f(2x)在定义域上也是偶函数,
∴当x∈(0,+∞)时,f(x)+f(2x)>0可满足题意,
∵当x∈(0,+∞)时,x3>0,
∴只需 ![]() +
+ ![]() +
+ ![]() +
+ ![]() >0,即
>0,即 ![]() >0,
>0,
∵a2x+ax+1>0,
∴(ax)2﹣1>0,解得a>1,
∴当a>1时,f(x)+f(2x)>0在定义域上恒成立
【解析】(1)由可推知f(﹣x)=f(x),从而可判断函数f(x)的奇偶性;(2)利用(1)知f(x)为偶函数,可知当x∈(0,+∞)时,x3>0,从而可判知,要使f(x)+f(2x)>0在其定义域上恒成立,只需当a>1时即可.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)═log2( ![]() +a).
+a).
(1)若f(1)<2,求实数a的取值范围;
(2)设函数g(x)=f(x)﹣log2[(a﹣4)x+2a﹣5],讨论函数g(x)的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
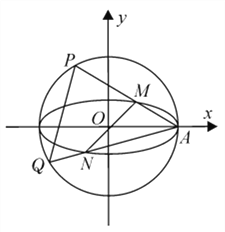
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() ,椭圆
,椭圆![]() ,
, ![]() 为椭圆
为椭圆![]() 的右顶点,过原点且异于
的右顶点,过原点且异于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 交于
交于![]() 两点,
两点, ![]() 在
在![]() 轴的上方,直线
轴的上方,直线![]() 与圆
与圆![]() 的另一交点为
的另一交点为![]() ,直线
,直线![]() 与圆
与圆![]() 的另一交点为
的另一交点为![]() ,
,
(1)若![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(2)设![]() 与
与![]() 的面积分别为
的面积分别为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不过第二象限的直线l:ax﹣y﹣4=0与圆x2+(y﹣1)2=5相切.
(1)求直线l的方程;
(2)若直线l1过点(3,﹣1)且与直线l平行,直线l2与直线l1关于直线y=1对称,求直线l2的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AF=BF,EC∥FD,FD⊥底面ABCD,M是AB的中点. 
(1)求证:平面CFM⊥平面BDF;
(2)点N在CE上,EC=2,FD=3,当CN为何值时,MN∥平面BEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=2cos(ωx+φ)(ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,点A、B分别为该部分图象的最高点与最低点,且这两点间的距离为4 ![]() ,则函数f(x)图象的一条对称轴的方程为( )
,则函数f(x)图象的一条对称轴的方程为( ) 
A.x= ![]()
B.x= ![]()
C.x=4
D.x=2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的偶函数,对x∈R,都有f(x﹣2)=f(x+2),且当x∈[﹣2,0]时,f(x)=( ![]() )x﹣1,若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0(a>1)恰有3个不同的实数根,则a的取值范围是( )
)x﹣1,若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0(a>1)恰有3个不同的实数根,则a的取值范围是( )
A.(2,3)
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车公司为了考查某4S店的服务态度,对到店维修保养的客户进行回访调查,每个用户在到此店维修或保养后可以对该店进行打分,最高分为10分.上个月公司对该4S店的100位到店维修保养的客户进行了调查,将打分的客户按所打分值分成以下几组:
第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10],得到频率分布直方图如图所示.
(I)求所打分值在[6,10]的客户的人数:
(II)该公司在第二、三组客户中按分层抽样的方法抽取6名客户进行深入调查,之后将从这6人中随机抽取2人进行物质奖励,求得到奖励的人来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四边形ABCD中, ![]() =(2,﹣2),
=(2,﹣2), ![]() =(x,y),
=(x,y), ![]() =(1,
=(1, ![]() ).
).
(1)若 ![]() ∥
∥ ![]() ,求x,y之间的关系式;
,求x,y之间的关系式;
(2)满足(1)的同时又有 ![]() ⊥
⊥ ![]() ,求x,y的值以及四边形ABCD的面积.
,求x,y的值以及四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com