
【题目】已知a∈R,函数f(x)═log2( ![]() +a).
+a).
(1)若f(1)<2,求实数a的取值范围;
(2)设函数g(x)=f(x)﹣log2[(a﹣4)x+2a﹣5],讨论函数g(x)的零点个数.
【答案】
(1)解:若f(1)<2,
则log2(1+a)<2,
即0<1+a<4,
解得:a∈(﹣1,3)
(2)解:令函数g(x)=f(x)﹣log2[(a﹣4)x+2a﹣5]=0,
则f(x)=log2[(a﹣4)x+2a﹣5],
即 ![]() +a=(a﹣4)x+2a﹣5,
+a=(a﹣4)x+2a﹣5,
即(a﹣4)x2+(a﹣5)x﹣1=0,
① 当a=4时,方程可化为:﹣x﹣1=0,解得:x=﹣1,
此时 ![]() +a=(a﹣4)x+2a﹣5=3,满足条件,
+a=(a﹣4)x+2a﹣5=3,满足条件,
即a=4时函数g(x)有一个零点;
②当(a﹣5)2+4(a﹣4)=0时,a=3,方程可化为:﹣x2﹣2x﹣1=0,
此时 ![]() +a=(a﹣4)x+2a﹣5=2,满足条件,
+a=(a﹣4)x+2a﹣5=2,满足条件,
即a=3时函数g(x)有一个零点;
③当(a﹣5)2+4(a﹣4)>0时,a≠3,
方程有两个根,x=﹣1,或x= ![]() ,
,
当x=﹣1时, ![]() +a=(a﹣4)x+2a﹣5=a﹣1,当a>1时,满足条件,
+a=(a﹣4)x+2a﹣5=a﹣1,当a>1时,满足条件,
当x= ![]() 时,
时, ![]() +a=(a﹣4)x+2a﹣5=
+a=(a﹣4)x+2a﹣5= ![]() ,当a
,当a ![]() 时,满足条件,
时,满足条件,
a≤ ![]() 时,函数g(x)无零点;
时,函数g(x)无零点;
![]() <a≤1时,函数g(x)有一个零点;
<a≤1时,函数g(x)有一个零点;
a>1且a≠3且a≠4时函数g(x)有两个零点
【解析】(1)若f(1)<2,则log2(1+a)<2,即0<1+a<4,解得实数a的取值范围;(2)令函数g(x)=f(x)﹣log2[(a﹣4)x+2a﹣5]=0,即 ![]() +a=(a﹣4)x+2a﹣5,即(a﹣4)x2+(a﹣5)x﹣1=0,分类讨论方程根的个数,可得不同情况下函数g(x)的零点个数.
+a=(a﹣4)x+2a﹣5,即(a﹣4)x2+(a﹣5)x﹣1=0,分类讨论方程根的个数,可得不同情况下函数g(x)的零点个数.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,M,N分别是BC1 , CD1的中点,则下列说法错误的是( ) 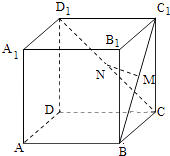
A.MN与CC1垂直
B.MN与AC垂直
C.MN与BD平行
D.MN与A1B1平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cos
=(cos ![]() ,sin
,sin ![]() ),
), ![]() =(cos
=(cos ![]() ,﹣sin
,﹣sin ![]() ),函数f(x)=
),函数f(x)= ![]()
![]() ﹣m|
﹣m| ![]() +
+ ![]() |+1,x∈[﹣
|+1,x∈[﹣ ![]() ,
, ![]() ],m∈R.
],m∈R.
(1)当m=0时,求f( ![]() )的值;
)的值;
(2)若f(x)的最小值为﹣1,求实数m的值;
(3)是否存在实数m,使函数g(x)=f(x)+ ![]() m2 , x∈[﹣
m2 , x∈[﹣ ![]() ,
, ![]() ]有四个不同的零点?若存在,求出m的取值范围;若不存在,说明理由.
]有四个不同的零点?若存在,求出m的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年9月,第22届鲁台经贸洽谈会在潍坊鲁台会展中心举行,在会展期间某展销商销售一种商品,根据市场调查,每件商品售价x(元)与销量t(万元)之间的函数关系如图所示,又知供货价格与销量呈反比,比例系数为20.(注:每件产品利润=售价﹣供货价格) 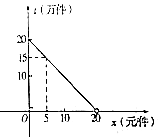
(1)求售价15元时的销量及此时的供货价格;
(2)当销售价格为多少时总利润最大,并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解心肺疾病是否与年龄相关,现随机抽取80名市民,得到数据如下表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
大于40岁 | 16 | ||
小于或等于40岁 | 12 | ||
合计 | 80 |
已知在全部的80人中随机抽取1人,抽到不患心肺疾病的概率为 ![]()
下面的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
(1)请将2×2列联表补充完整;
(2)能否在犯错误的概率不超过0.025的前提下认为患心肺疾病与年龄有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数 ![]() ,x∈R的图象,只需把函数y=2sinx,x∈R的图象上所有的点( )
,x∈R的图象,只需把函数y=2sinx,x∈R的图象上所有的点( )
A.向左平移 ![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 ![]() 倍纵坐标不变)
倍纵坐标不变)
B.向右平移 ![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 ![]() 倍(纵坐标不变)
倍(纵坐标不变)
C.向左平移 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
D.向右平移 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() +
+ ![]() )x3(a>0,a≠1).
)x3(a>0,a≠1).
(1)讨论函数f(x)的奇偶性;
(2)求a的取值范围,使f(x)+f(2x)>0在其定义域上恒成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com